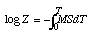
It is known that the action of acids on cane sugar, which rotates the plane of polarized light passing through its solution to the right, converts it into fruit sugar, which rotates the plane to the left. Since now with the aid of a polarization apparatus, the Soleil double plate, readings of how far this change has proceeded can be made with great ease in an instant, it seemed to me to offer the possibility of finding the laws of the process which we are discussing. It is also a problem of interest to establish in this special case. However, this is certainly only one member of a greater series of phenomena which all follow general laws of nature.
...
Under the final assumption[1], however, the formula which expresses the chemical process can be developed in the following way:
Using the symbols introduced above,[2] dZ is the sugar loss in the time interval dT, and it is assumed that this is determined by the formula
- dZ/dT = MZSin which M, as before, is the mean value of the infinitely small amount of sugar units which are changed during the time element by the action of the amount of acid present.
The above equation gives by integration
or since, as has already been shown, S is constant, and on the other hand M also is independent of Z and therefore also of T, as will later be shown by experiment,
log Z = -MST + CFor T = 0, Z = Z0, therefore,
log Z0 - log Z = MST, or Z = Z0e-MST.
...
According to the preceding work, I can therefore use the formula developed earlier
log Z0 - log Z = MSTin the study now made.
(log Z - log Z0)/MS
The convenient half-Briggsian logarithms could be used without disadvantage, since we are concerned only with the ratio of the numbers to each other and not with their absolute values. The figures thus obtained are collected in Table III.
| Table III | |||
|---|---|---|---|
| T | Rotation | [log Z0 - log Z)/MS[3] | t |
| 46°, 75 before mixing | |||
| 8 h. | Mixing of acid with sugar solution | ||
| 8 h. 15' | +43°, 75 | 15°5 | |
| " 30 | +41 | ||
| " 45 | +38, 25 | ||
| 9 h. | +35, 75 | 0.0801671 | |
| 9 h. 15 | +33, 25 | ||
| 9 h. 30 | +30, 75 | ||
| 9 h. 45 | +28, 25 | ||
| 10 h. | +26 | 0.1661271 | |
| 10 h. 30 | +22 | ||
| 11 h. | +18, 25 | 0.2504869 | |
| 11 h. 30 | +15 | ||
| 12 h. | +11, 5 | 0.3393678 | |
| 12 h. 30 | +8, 25 | ||
| 1 h. 30 | +2, 75 | 0.4882238 | 18° |
| 2 h. 30 | -1, 75 | 0.5859208 | 16° |
| 3 h. 30 | -4, 5 | 0.6628879 | |
| 4 h. 30 | -7 | 0.7470561 | 15° |
| 5 h. 30 | -8, 75 | 0.8173016 | |
| 6 h. 30 | -10 | 0.8752936 | 14°5 |
As can be seen, the values found during the time which passed are very nearly proportional, from which the correctness of the formula Z = Z0e-MST in relation to time T is established. The small deviation from proportionality is explained by the irregularities of temperature, to which I will return later. A necessary conclusion from the equation, moreover, is that when T = °, can become zero, hence the inversion of the sugar, strictly speaking, is never ended, although due to the smallness of the residue, very soon a further decrease is not noticeable.
we get the following values
| M = 0.0204467 . 1/5 | (t 15°,5) |
| M = 0.0197215 " | |
| M = 0.0204460 " | |
| M = 0.0195529 " | |
| M = 0.0204748 " | |
| M = 0.0214880 " | |
| M = 0.0226069 " | |
| M = 0.0213903 " | |
| M = 0.0210030 " | |
| M = 0.0202667 " | |
| M = 0.0241737 " | |
| M = 0.0240091 " | |
| M = 0.0252094 " | t 18° (maximum temperature) |
| M = 0.0244242 " | |
| M = 0.0192418 " | |
| M = 0.0210170 " | |
| M = 0.0175614 " | |
| M = 0.0142906 " | t 14°,5 |
The independence of the value of M of the amount of sugar will be further indicated by a special study. This was found in each of the studies carried out simultaneously and at the same temperatures, in which, besides the amount of acid S and the amount of water W, M by the formula log Z0 - log Z = MST was found constant. The detailed conditions and results are given in Table IV.
| Table IV | |||||
|---|---|---|---|---|---|
| Z0 | Anhydrous HNO3 | W | T | D | M |
| S | |||||
| 45° | 0.281 g. | 7.542 g. | 13 h. | +4°,25 | 0.1240 |
| 36 | " | " | " | +3 | 0.1267 |
| 27 | " | " | " | +2 | 0.1290 |
| 18 | " | " | " | +1,25 | 0.1301 |
| 9 | " | " | " | +3 | 0.1201 |
Z = Z0 - (Z0-D)/(1+m)
[2][Z = concentration of sugar, S = concentration of acid. --L&K]
[3]Z is found from the observed rotation; D, by the formula Z = Z0 - (Z0 -D)/(1 + m)
 Back to the list of selected historical papers.
Back to the list of selected historical papers. Back to the top of Classic Chemistry.
Back to the top of Classic Chemistry.