Leonor Michaelis (1875-1940) and Maud Leonora Menten (1879-1960)
The kinetics of invertase activity
Biochemische Zeitschrift 49, 333 (1913) [as translated and excerpted in Mikulás Teich, A Documentary History of Biochemistry, 1770-1940 (Rutherford, NJ: Fairleigh Dickinson University Press, 1992)]
...
3. The equation of the reaction of fermentative splitting of cane sugar
... we are now in a better position to solve the old problem of the reaction equation of invertase in a rational manner and without help of more than one arbitrary constant. Until now V. Henri has come nearest of all authors to this solution, and we can consider our derivation as a further modification, on the grounds of newly acquired knowledge, of the Henri derivation.
The fundamental assumption of this deduction is this, that the rate of breakdown at any moment is proportional to the concentration of the sucrose-invertase compound; and that the concentration of this compound at any moment is determined by the concentration of the ferment, of the sucrose, and also of the split products capable of binding of the ferment. However whilst Henri brought into consideration an 'affinity constant of the split products', we operated particularly with the dissociation constant of the sucrose-ferment combination, k = 1/60, with that of the fructose-ferment combination, k1 = 1/17, and with that of the glucose-ferment combination, k2 = 1/11.
We apply besides the following symbols:
| Φ = | the total ferment concentration
|
| φ = | the concentration of the sucrose-ferment combination
|
| υ1 = | the concentration of the fructose-ferment combination
|
| υ2 = | the concentration of the glucose-ferment combination
|
| S = | the concentration of the sucrose | 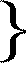 | that is to say, the concentration of the sugar in question in the free state which however is practically equal to that of the total sugar in question.
|
| F = | the concentration of the fructose
|
| G = | the concentration of the glucose
|
Since upon splitting just as much fructose as glucose is formed, G is always equal to F.
Now in any moment according to the law of mass action[1]
| (1) | S(Φ - φ -υ1 - υ2) = kφ
|
| (2) | F(Φ - φ -υ1 - υ2) = k1υ1
|
| (3) | G(Φ - φ -υ1 - υ2) = k2υ2
|
From (1) it follows
| (4) | φ = S(Φ -υ1 - υ2)/(S + k) |
We can eliminate υ1 and υ2 if we first find by division of (2) and (3):
υ2 = (k1/k2).υ1 ,
and further by division of (1) and (3)
υ1 = (k/k1).φ.(F/S) ,
so that
υ1 + y2 = k.φ.(F/S)(1/k1 + 1/k2) .
Let us refer next to the abbreviation
1/k1 + 1/k2 = q ,
so that
υ1 + y2 = k.q.φF/S .
This gives, substituted in (4) and solved for φ,
Now we can arrive at the differential equation. If a is the initial amount of sucrose, t the time, x the amount of fructose or glucose present at time t, that is a - x the amount of sucrose still present at time t, then the breakdown rate at time t is defined by
vt = dx/dt .
According to assumption this is proportional to φ, so that our differential equation with use of equation (4) runs:
| (5) | dx/dt = C . (a - x)/[a + k - x(1 - kq)] |
where C represents the single arbitrary constant; and indeed this is proportional to the amount of ferment.
The general integral of the equation is given without mathematical difficulty:
C . t = (1 - kq)x - k(1 + aq) ln (a - x) + constant .
For the elimination of the integration constants we give below the corresponding equation for the initial state of the process, for which x = 0 and t = 0:
0 = k(1 + aq) . ln a + constant ,
and find finally by subtraction of the two last equations the definite integral:
| (6) | C . t = k(1 + aq) . ln [a/(a - x)] + (1 - kq)x |
or with introduction of the value for q:
(k/t)(1/a + 1/k1 + 1/k2) . a ln [a/(a - x)] + (k/t) (1/k - 1/k1 - 1/k2)x = C .
Now one can as well include k in the constant on the right side and obtain:
| (7) | (1/t)(1/a + 1/k1 + 1/k2) . a ln [a/(a - x)] + (1/t) (1/k - 1/k1 - 1/k2)x = constant |
It is characteristic for this function as for that of Henri, that it gives by superposition a linear and a logarithmic function of the type
| (8) | m . ln [a/(a - x)] + n. x = t . constant |
where m and n have the meaning apparent from the previous equation; they are factors whose magnitude is determined by the particular dissociation constants and the initial amount of sugar.
If we use the values of k, k1, and k2 obtained by us at the experimental temperature of 25°, we have
| (9) | (1/t) (1 + 28a) . 2,303 log10 [a/(a - x)] + (1/t) . 32 . x = constant |
Instead of log [a/(a - x)] we write more simply for the calculation - log (1 - x/a) .
This constant must be proportional to the ferment concentration. That it is so appears from all earlier investigations, and especially it was shown by L. Michaelis and H. Davidson ... that an equation of the form
| (10) | amount of ferment x time = f(a,x) |
strictly proved correct. The function left undetermined on the right-hand side of this equation is given a definite form by means of our equation (8), otherwise nothing is altered and one sees forthwith by comparison of (8) and (10) that the constant of equation (8) must be proportional to the ferment concentration.
Thus it is superfluous to test the correctness of equation (9) with changing amounts of ferment; but it must be tested once more whether this constant remains the same with the same ferment amount but changing sugar amounts; and above all whether during a single experiment it is independent of the time. We use now ... the values of x, which hitherto we described in arbitrary polarimetric units of measure, and have to convert them into moles. We make use in this of the assumption that the theoretical final rotation of a sucrose solution, which at first rotates m°, amounts to -0.313 m°.
| Time (t) | x/a | K | Mean
|
| | I. Sucrose 0,333 n.
|
| 7 | 0,0164 | 0,0496
|
| 14 | 0,0316 | 0,0479
|
| 26 | 0,0528 | 0,0432
|
| 49 | 0,0923 | 0,0412
|
| 75 | 0,1404 | 0,0408
|
| 117 | 0,2137 | 0,0407
|
| 1052 | 0,9834 | [0,0498] | 0,0439
|
| | II. Sucrose 0,1667 n.
|
| 8 | 0,0350 | 0,0444
|
| 16 | 0,0636 | 0,0446
|
| 28 | 0,1080 | 0,0437
|
| 52 | 0,1980 | 0,0444
|
| 82 | 0,3000 | 0,0445
|
| 103 | 0,3780 | 0,0454 | 0,0445
|
| | III. Sucrose 0,0833 n.
|
| 49,5 | 0,352 | 0,0482
|
| 90,0 | 0,575 | 0,0447
|
| 125,0 | 0,690 | 0,0460
|
| 151,0 | 0,766 | 0,0456
|
| 208,0 | 0,900 | 0,0486 | 0,0465
|
| | IV. Sucrose 0,0416 n.
|
| 10,25 | 0,1147 | 0,0406
|
| 30,75 | 0,3722 | 0,0489
|
| 61,75 | 0,615 | 0,0467
|
| 90,75 | 0,747 | 0,0438
|
| 112,70 | 0,850 | 0,0465
|
| 132,70 | 0,925 | 0,0443
|
| 154,70 | 0,940 | 0,0405
|
| 1497,00 | 0,972 | [0,0514] | 0,0445
|
| | V. Sucrose 0,0208 n.
|
| 17 | 0,331 | 0,0510
|
| 27 | 0,452 | 0,0464
|
| 38 | 0,611 | 0,0500
|
| 62 | 0,736 | 0,0419
|
| 95 | 0,860 | [0,0388]
|
| 1372 | 0,990 | [0,058] | 0,0474
|
| Average mean value 0,0454. |
The constant is in all experiments so consistent and, apart from slight fluctuations, shows no 'slant' either with time or with sugar concentration, that we can consider it as satisfactorily constant.
[1]The derivation as presented here differs substantially from that printed in Teich. I hope I have eliminated the errors (φ and υ for υ, for example). --CJG
 Back to the list of selected historical papers.
Back to the list of selected historical papers.
 Back to the top of Classic Chemistry.
Back to the top of Classic Chemistry.
 Back to the list of selected historical papers.
Back to the list of selected historical papers. Back to the top of Classic Chemistry.
Back to the top of Classic Chemistry.