The case of the electron raises several interesting points about the discovery process. Clearly, the characterization of cathode rays was a process begun long before Thomson's work, and several scientists made important contributions. In what sense, then, can Thomson be said to have discovered the electron? After all, he did not invent the vacuum tube or discover cathode rays. Discovery is often a cumulative process. The credited discoverer makes crucial contributions to be sure, but often after fundamental observations have been made and tools invented by others. Thomson was not the only physicist to measure the charge-to-mass ratio of cathode rays in 1897, nor the first to announce his results. (See Pais 1986.) But Thomson did carry out this measurement and (later) the measurement of the particles's charge, and he recognized its importance as a constituent of ordinary matter.
The first place in which corpuscles were detected was a highly exhausted tube[3] through which an electric discharge was passing. When an electric discharge is sent through a highly exhausted tube, the sides of the tube glow with a vivid green phosphorescence. That this is due to something proceeding in straight lines from the cathode--the electrode where the negative electricity enters the tube--can be shown in the following way (the experiment is one made many years ago by Sir William Crookes[4]): A Maltese cross made of thin mica is placed between the cathode and the walls of the tube.[5] When the discharge is past, the green phosphorescence no longer extends all over the end of the tube, as it did when the cross was absent. There is now a well-defined cross in the phosphorescence at the end of the tube; the mica cross has thrown a shadow and the shape of the shadow proves that the phosphorescence is due to something travelling from the cathode in straight lines, which is stopped by a thin plate of mica. The green phosphorescence is caused by cathode rays[6] and at one time there was a keen controversy as to the nature of these rays. Two views were prevalent: one, which was chiefly supported by English physicists, was that the rays are negatively electrified bodies shot off from the cathode with great velocity; the other view, which was held by the great majority of German physicists, was that the rays are some kind of ethereal vibration or waves.[7]
The arguments in favour of the rays being negatively charged particles are primarily that they are deflected by a magnet in just the same way as moving, negatively electrified particles. We know that such particles, when a magnet is placed near them, are acted upon by a force whose direction is at right angles to the magnetic force, and also at right angles to the direction in which the particles are moving.[8]
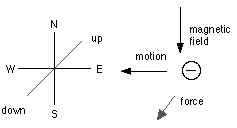
Thus, if the particles are moving horizontally from east to west, and the magnetic force is horizontal from north to south, the force acting on the negatively electrified particles will be vertical and downwards.[9]
When the magnet is placed so that the magnetic force is along the direction in which the particle is moving, the latter will not be affected by the magnet.
The next step in the proof that cathode rays are negatively charged particles was to show that when they are caught in a metal vessel they give up to it a charge of negative electricity. This was first done by Perrin.[10] This experiment was made conclusive by placing the catching vessel out of the path of the rays, and bending them into it by means of a magnet, when the vessel became negatively charged.[11]
By exhausting the vacuum tube until there was only an exceedingly small quantity of air left in to be made a conductor, I was able to get rid of this effect and to obtain the electric deflection of the cathode rays.[14] This deflection had a direction which indicated a negative charge on the rays.
Thus, cathode rays are deflected by both magnetic and electric forces, just as negatively electrified particles would be.
Hertz showed, however, that cathode particles possess another property which seemed inconsistent with the idea that they are particles of matter, for he found that they were able to penetrate very thin sheets of metal, e.g. pieces of gold leaf, and produce appreciable luminosity on glass behind them.[15] The idea of particles as large as the molecules of a gas passing through a solid plate was a somewhat startling one,[16] and this led me to investigate more closely the nature of the particles which form the cathode rays.
The principle of the method used is as follows: When a particle carrying a charge e is moving with velocity v across the lines of force in a magnetic field, placed so that the lines of magnetic force are at right angles to the motion of the particle, then, if H is the magnetic force, the moving particle will be acted on by a force equal to Hev. This force acts in the direction which is at right angles to the magnetic force and to the direction of the motion of the particle. If also we have an electric field of force X, the cathode ray will be acted upon by a force Xe. If the electric and magnetic fields are arranged so that they oppose each other, then, when the force Hev due to the magnetic field is adjusted to balance the force due to the electric field Xe, the green patch of phosphorescence due to the cathode rays striking the end of the tube will be undisturbed, and we have
Hev = Xeor
v = X/H .
Thus if we measure, as we can do without difficulty, the values of X and H when the rays are not deflected, we can determine the value of v, the velocity of the particles.[17] In a very highly exhausted tube this may be 1/3 the velocity of light, or about 60,000 miles per second; in tubes not so highly exhausted it may not be more than 5,000 miles per second, but in all cases when the cathode rays are produced in tubes their velocity is much greater than the velocity of any other moving body with which we are acquainted. It is, for example, many thousand times the average velocity with which the molecules of hydrogen are moving at ordinary temperatures, or indeed at any temperature yet realized.[18]
Thus the displacement of the patch of phosphorescence where the rays strike the glass is equal to
(1/2) (Xe/m) (l2/v2) .We can easily measure this displacement d, and we can thus find e/m from the equation[19]
e/m = (2d/X) (v2/l2) .
The results of the determinations of the values of e/m made by this method are very interesting, for it is found that, however the cathode rays are produced, we always get the same value of e/m for all the particles in the rays. We may, for example, by altering the shape of the discharge tube and the pressure of the gas in the tube, produce great changes in the velocity of the particles, but unless the velocity of the particles becomes so great that they are moving nearly as fast as light, when other considerations have to be taken into account, the value of e/m is nearly constant.[20] The value of e/m is not merely independent of the velocity. What is even more remarkable is that it is independent of the kind of electrodes we use and also of the kind of gas in the tube. The particles which form the cathode rays must come either from the gas in the tube or from the electrodes; we may, however, use any kind of substance be please for the electrodes and fill the tube with gas of any kind and yet the value of e/m will remain unaltered.[21]
This constant value, when we measure e/m in the c.g.s. system of magnetic units, is equal to about 1.7x107. If we compare this with the value of the ratio of the mass to the charge of electricity carried by any system previously known, we find that it is of quite a different order of magnitude. Before the cathode rays were investigated, the charged atom of hydrogen met with in the electrolysis of liquids was the system which had the greatest known value of e/m, and in this case the value is only 104, hence for the corpuscle in the cathode rays the value of e/m is 1,700 times the value for the corresponding quantity for the charged hydrogen atom. This discrepancy must arise in one or other of two ways; either the mass of the corpuscle must be very small compared with that of the atom of hydrogen, which until quite recently was the smallest mass recognized in physics, or else the charge on the corpuscle must be very much greater than that on the hydrogen atom. Now it has been shown by a method which I shall shortly describe, that the electric charge is practically the same in the two cases; hence we are driven to the conclusion that the mass of the corpuscle is only about 1/1,700 of that of the hydrogen atom. Thus the atom is not the ultimate limit to the subdivision of matter; we may go further and get to the corpuscle, and at this stage the corpuscle is the same from whatever source it may be derived.
Corpuscles are also given out by metals and other bodies, but especially by the alkali metals, when these are exposed to light.[23]
They are being continually given out in large quantities and with very great velocities by radioactive substances such as uranium and radium;[24] they are produced in large quantities when salts are put into flames, and there is good reason to suppose that corpuscles reach us from the sun.
The corpuscle is thus very widely distributed, but wherever it is found, it preserves its individuality, e/m being always equal to a certain constant value.
The corpuscle appears to form a part of all kinds of matter under the most diverse conditions; it seems natural therefore to regard it as one of the bricks of which atoms are built up.[25]
When charged particles are present in the gas, Wilson showed that a much smaller amount of cooling is sufficient to produce the fog, a four-fold supersaturation being all that is required when the charged particles are those which occur in a gas when it is in a state in which it conducts electricity. Each of the charged particles becomes the centre round which a drop of water forms; the drops form a cloud, and thus the charged particles, however small to begin with, now become visible and can be observed.
The effect of the charged particles on the formation of a cloud can be shown very distinctly by the following experiment:
A vessel which is in contact with water is saturated with moisture at the temperature of the room. This vessel is in communication with a cylinder in which a large piston slides up and down. The piston to begin with is at the top of its travel; by suddenly exhausting the air from below the piston, the air in the vessel will expand very quickly. When, however, air expands, it gets cool; thus the air in the vessel previously saturated is now supersaturated. If there is no dust present, no deposition of moisture will take place, unless the air is cooled to such a low temperature that the amount of moisture required to saturate it is only about 1/8 of that actually present.
Now the amount of cooling, and therefore of supersaturation, depends upon the travel of the piston; the greater the travel the greater the cooling. Suppose the travel is regulated so that the supersaturation is less than eightfold and greater than fourfold. We now free the air from dust by forming cloud after cloud in the dusty air; as the clouds fall they carry the dust down with them, just as in nature the air is cleared by showers. We find at last that when we make the expansion no cloud is visible.[28]
The gas is now made in a conducting state by bringing a little radium near the vessel; this fills the gas with large quantities of both positively and negatively electrified particles. On making the expansion now an exceedingly dense cloud is formed. That this is due to the electrification in the gas can be shown by the following experiment:
Along the inside walls of the vessel we have two vertical insulated plates which can be electrified. If these plates are charged, they will drag the electrified particles out of the gas as fast as they are formed, so that in this way we can get rid of, or at any rate largely reduce, the number of electrified particles in the gas. If the expansion is now made with the plates charged before bringing up the radium, there is only a small cloud formed.[29]
We can use the drops to find the charge on the particles, for when we know the travel of the piston, we can deduce the amount of supersaturation, and hence the amount of water deposited when the cloud forms. The water is deposited in the form of a number of small drops all of the same size; thus the number of drops will be the volume of the water deposited divided by the volume of one of the drops. Hence, if we find the volume of one of the drops, we can find the number of drops which are formed round the charged particles. If the particles are not too numerous, each will have a drop round it, and we can thus find the number of electrified particles.[30]
From the rate at which the drops slowly fall we can determine their size. In consequence of the viscosity or friction of the air small bodies do not fall with a constantly accelerated velocity, but soon reach a speed which remains uniform for the rest of the fall; the smaller the body the slower this speed. Sir George Stokes has shown that v, the speed at which a drop of rain falls, is given by the formula
v = (2/9) (ga2/μ)where a is the radius of the drop, g the acceleration due to gravity, and μ the coefficient of viscosity of the air.
If we substitute the values of g and μ, we get
v = 1.28x106 x a2Hence if we measure v we can determine a, the radius of the drop.
We can in this way find the volume of a drop, and may therefore, as explained above, calculate the number of drops and therefore the number of electrified particles.
It is a simple matter to find by electrical methods the total quantity of electricity on these particles; and hence, as we know the number of particles, we can deduce at once the charge on each particle.
This was the method by which I first determined the charge on the particle;[31] H. A. Wilson has since used a simpler method founded on the following principles: C. T. R. Wilson has shown that the drops of water condense more easily on negatively electrified particles than on positively electrified ones. Thus, by adjusting the expansion, it is possible to get drops of water round the negative particles and not round the positive; with this expansion, therefore, all the drops are negatively electrified. The size of these drops and therefore their weight can, as before, be determined by measuring the speed at which they fall under gravity. Suppose now, that we hold above the drops a positively electrified body; then, since the drops are negatively electrified, they will be attracted towards the positive electricity, and thus the downward force on the drops will be diminished and they will not fall so rapidly as they did when free from electrical attraction. If we adjust the electrical attraction so that the upward force on each drop is equal to the weight of the drop, the drops will not fall at all, but will, like Mahomet's coffin[32], remain suspended between heaven and earth. If then we adjust the electrical force until the drops are in equilibrium and neither fall nor rise, we know that the upward force on each drop is equal to the weight of the drop, which we have already determined by measuring the rate of fall when the drop was not exposed to any electrical force. If X is the electrical force, e the charge on the drop, and w its weight, we have, when there is equilibrium,
Xe = wSince X can easily be measured and w is known, we can use this relation to determine e, the charge on the drop. The value of e, found by these methods, is 3.1x10-10 electrostatic units, or 10-20 electromagnetic units. This value is the same as that of the charge carried by a hydrogen atom in the electrolysis of dilute solutions, and approximate value of which has been long known.
It might be objected that the charge measured in the preceding experiments is the charge on a molecule or collection of molecules of the gas, and not the charge on a corpuscle.[33]
This objection does not, however, apply to another form in which I tried the experiment, where the charges on the corpuscles were got, not by exposing the gas to the effects of radium, but by allowing ultraviolet light to fall on a metal plate in contact with the gas. In this case, as experiments made in a very high vacuum show, the electrification, which is entirely negative, escapes from the metal in the form of corpuscles. When a gas is present, the corpuscles strike against the molecules of the gas and stick to them.
Thus, though it is the molecules which are charged, the charge on a molecule is equal to the charge on a corpuscle, and when we determine the charge on the molecules by the methods I have just described, we determine the charge carried by the corpuscle.
The value of the charge when the electrification is produced by ultraviolet light is the same as when the electrification is produced by radium.[34]
We have just seen that e, the charge on the corpuscle, is in electromagnetic units equal to 10-20, and we have previously found that e/m, m being the mass of a corpuscle, is equal to 1.7x107, hence m = 6x10-28 grammes.
We can realize more easily what this means if we express the mass of the corpuscle in terms of the mass of the atom of hydrogen.
We have seen that for the corpuscle e/m = 1.7x107. If E is the charge carried by an atom of hydrogen in the electrolysis of dilute solutions, and M is the mass of the hydrogen atom, E/M = 104; hence e/m = 1,700 E/M.
We have already stated that the value of e found by the preceding methods agrees well with the value of E which has long been approximately known. Townsend has used a method in which the value of e/E is directly measured, and has shown in this way also that e equal to E. Hence, since e/m = 1,700 E/M, we have M = 1,700 m, i.e., the mass of a corpuscle is only about 1/1,700 part of the mass of the hydrogen atom.[35]
In all known cases in which negative electricity occurs in gases at very low pressures, it occurs in the form of corpuscles, small bodies with an invariable charge and mass. The case is entirely different with positive electricity.[36]
[2]Both of these properties of electrons, their very low mass and their widespread occurrence, had profound effects on scientists' understanding of matter. The small mass indicated that pieces of matter existed which were smaller (lighter) than the smallest atom yet known by a factor of 1000. The formation of the same small particles from a wide variety of sources suggested that those particles were common constituents of atoms, and not an exotic form of matter. The two conclusions taken together imply that even the smallest atoms have component parts, that they are not structureless or indivisible. (The picture of structureless atoms as the basic building blocks of atoms was rather widely, but by no means universally held at the close of the 19th century. Some scientists, including Thomson, believed that atoms had structure, whether or not they were divisible. And a minority still regarded atoms themselves as unproved or as useful fictions.)
[3]Exhausted is used here in the sense of evacuated, that is, a glass tube from which the gas had been pumped. Vacuum tube would be another appropriate term for such a device.
[4]William Crookes was a productive researcher and highly original and speculative thinker in many areas of physics and chemistry. (See chapter 14, note 29.) His work on electrical discharges in vacuum tubes in the late 1870s laid some foundational work on which Thomson built; indeed, his "Crookes tubes" were widely used in cathode ray research.
[5]See photo of Crookes' Maltese cross tube (at the Science Museum, London). A Maltese cross has arms of equal length and is flared at the ends. The cross was used as a heraldic symbol of the medieval crusading Knights of Malta. The advantage of employing this shape in the present experiment is that it is simple enough to fashion, yet complex enough to throw quite distinctive shadows. Mica is an aluminum silicate mineral readily split into thin transparent sheets.
[6]Cathode rays were known for much of the 19th century. Descriptions of electrical discharges in partially evacuated containers date to the late 18th century. Productive study of the rays began in the 1850s, when Johann Geissler improved the vacuum pump and vacuum tubes and Julius Plücker made systematic observations using those tubes. Eugen Goldstein coined the term cathode rays in 1876. They were called cathode rays because they were emitted from the cathode of the vacuum tube. The term cathode ray is obsolete; today the rays would be described as a beam of electrons. See Anderson 1964 or Pais 1986 for detailed chronologies of cathode ray research.
Even though one rarely hears of cathode rays anymore, cathode ray tubes (CRTs) were specialized and sophisticated versions of vacuum tubes widely used for video display in television sets, computer monitors, oscilloscopes, and other devices throughout the second half of the 20th century. CRTs shoot electrons at a screen coated with phosphors, which glow when they are struck by the electron beam. (Thomson's tube glowed green because of the kind of glass it was made of; other materials glow other colors when struck by electrons.) CRTs use magnetic fields to make the electron beam rapidly scan the tube to produce an image. (In the mid-19th century, Plücker noticed that magnetic fields distort the glow of cathode rays.) Big projection screen TVs and flat-screen monitors have largely displaced CRTs for video monitors in the 21st century.
[7]The two alternatives represent two main categories of physical reality. The key word in the first alternative, suggested in 1871 by Cromwell Varley, is bodies. That is, the English physicists thought cathode rays were a stream of fast-moving particles and therefore matter. The key word in the second alternative, proposed in 1880 by Goldstein, is waves. That is, the German physicists thought cathode rays were a wave phenomenon, perhaps something like light and other related electromagnetic energy. At the end of the 19th century, physicists considered waves and particles two distinct alternatives; something could not be both a wave and a particle. The sharp distinction between waves and particles blurred during the first quarter of the 20th century; now physicists routinely refer to wavelike properties of particles and particle-like properties of waves. In fact, the electron turned out to be a particle which is involved in several wave-like phenomena (but that's another story).
[8]Thomson's line of argument, essentially, is that one can tell cathode rays are charged particles because they behave the way charged particles behave. The behavior of charged particles in magnetic fields is just one of several consequences that can be inferred from the hypothesis that cathode rays consist of charged particles.
There is a deep connection between electricity and magnetism, despite their seeming at first to be distinct phenomena. The fact that magnetic fields can deflect moving electrical charges is one of the manifestations of this deep connection. A more practical aspect of the relationship between electricity and magnetism is that moving electric charges can give rise to magnetic fields, and changing magnetic fields can set electric charges into motion. This connection is the basis for the generation of electrical current at power plants and for the design of electrical motors. The English scientists Michael Faraday (1791-1867) and James Clerk Maxwell (1831-1879; see portrait in Early History of Radio Astronomy, Frank D. Ghigo, National Radio Astronomy Observatory) were instrumental in unraveling the connections between electricity and magnetism.
[9]The diagram below shows the directions involved: down is into the screen and up is out of the screen.

[10]Jean Baptiste Perrin (1870-1942; see photo and biographical information at the Nobel Foundation website) carried out this collection of cathode rays in 1895 [Perrin 1895]. Perrin was awarded the Nobel Prize in physics in 1926 for his work on the random motion of atoms (known as Brownian movement), which he began in 1908.
[11]Thomson has so far described two independent lines of evidence to support the hypothesis that cathode rays are particles that carry a negative electrical charge. First, cathode rays exposed to a magnetic field act just like negative electric charges in motion would act. Second, a metal bombarded by cathode rays acquires a negative electrical charge. Thomson himself made the collection experiment conclusive and particularly elegant, by combined both lines of evidence (using magnetic deflection to guide the particles onto the metal collector) [Thomson 1897a, 1897b].
[12]If cathode rays are electrically charged particles, they should behave like charged particles in all respects; in particularly, they ought to be deflected when exposed to an electric field. In 1883, German physicist Heinrich Hertz looked for deflection of cathode rays by electric fields but found no deflection.
Hertz (1857-1894; see photo in Early History of Radio Astronomy, Frank D. Ghigo, National Radio Astronomy Observatory) is best known for his work demonstrating the existence of electromagnetic waves, in particular radio waves. The frequencies of radio waves are measured in units named after him; one hertz is one cycle per second. Frequencies in the FM band are in the neighborhood of 100 megahertz (millions of hertz), and AM frequencies are in the neighborhood of 1000 kilohertz (thousands of hertz).
[13]Thomson said that the passage of cathode rays made the gas in the tube capable of conducting electricity. A modern scientist would say that the cathode rays (electrons) ionize the gas molecules, breaking off additional electrons from the atoms and leaving positively charged ions. (Ions are electrically charged atoms or molecules.) Indeed, Thomson presented this picture of ionization in 1899, not long after his characterization of cathode rays.
Electrostatic attraction would cause the ions to surround the electrons. Since each of the charged particles itself gives rise to an electric field, it was certainly plausible to think that an external electric field would hardly be felt by the surrounded cathode rays. If Thomson was right (and he was), his next task would be to reduce the screening effect of the ions or otherwise prove that their interference prevented electric deflection of the cathode rays. If not, the failure of electric deflection experiments could be interpreted as evidence against the idea that cathode rays were electrically charged particles.
[14]The demonstration that cathode rays were deflected by electric fields awaited a technological development, improvement in the techniques for achieving high vacua (extremely low pressures). As Thomson later recalled [Thomson 1936]:
"The absence of deflection on this view is due to the presence of gas--to the pressure being too high--thus the thing to do was to get a much higher vacuum. This was more easily said than done. The technique of producing high vacua in those days was in an elementary stage. The necessity of getting rid of gas condensed on the walls of the discharge tube, and on the metal of the electrodes by prolonged baking, was not realized. As this gas was liberated when the discharge passed through the tube, the vacuum deteriorated rapidly during the discharge, and the pumps then available were not fast enough to keep pace with this liberation. However, after running the discharge through the tube day after day without introducing fresh gas, the gas on the walls and electrodes got driven off and it was possible to get a much better vacuum. The deflection of the cathode rays by electric forces became quite marked, and its direction indicated that the particles forming the cathode rays were negatively electrified."
[15]I find it somewhat curious that Thomson fails to mention the student of Hertz who was awarded the Nobel Prize in physics one year before Thomson for his own work on cathode rays. Philipp Lenard (1862-1947; see photo at Wikimedia Commons) extended Hertz' work, conducting a series of experiments which involved measuring the penetrating power of the rays once they had passed through thin pieces of metal foil. Thomson referred to Lenard's work in detail in 1897 [Thomson 1897a, 1897b].
[16]At the time of Hertz' experiments, those who thought that cathode rays were charged particles had in mind charged gas molecules. Since gas molecules were known to be incapable of penetrating metal foils, no wonder this observation was "startling." The observation would be somewhat less startling if the rays were supposed to be particles much smaller than gas molecules.
[17]The design of this experiment illustrates an elegant indirect measurement and the use of mathematical formalism to derive inferences from observations. The measurement is indirect in that it determines the speed of the particle without measuring either distance or time. (Indeed, Thomson tried a more direct measurement of cathode ray velocity in 1894 [Thomson 1894], but it turned out to be unreliable.) The force a magnetic field exerts on a charged particle is proportional to the speed of the particle as well as its charge; thus, if that force could be measured the speed could be inferred. Thomson couldn't even quite measure the force, but he could arrange to balance the force with an electric field. Since the cathode rays made the glass tube glow where they hit it, the rays provided a visible means to tell then the magnetic and electric forces were in balance. When they were in balance, the two forces were equal. Then a single step of elementary algebra turned a mathematical statement about two equal forces into a formula for the velocity of the ray. Since the electric and magnetic field strengths were known and controlled by the experimenter, the velocity could be computed.
The figure below (from Thomson 1897b) shows a diagram of the apparatus including the plates for applying an electric field and a scale at the right end to measure deflection of the beam.
[18]In emphasizing how fast the rays are compared to forms of matter then known, Thomson does not stress that the rays are slow compared to light. But this observation is another piece of evidence against the hypothesis that the rays are electromagnetic waves, for those waves travel at the speed of light.
[19]This measurement of the charge to mass ratio (e/m) of the electron is also indirect, and it illustrates even better than the measurement of velocity the utility of algebraic language to make inferences. To paraphrase, an electric field with strength X applied perpendicular to the line of direction of the cathode rays will make the rays fall a distance d over the course of a flight of length l (essentially the length of the tube). The distance the rays will fall is given by:
d = 1/2gt2 ,where g is the acceleration and t the time of flight. Think of the above formula as a declarative sentence about the distance and its relationship to acceleration and time; the language of algebra expresses the relationship in a compact form. Next, Thomson substitutes for g the acceleration appropriate for an electric force (Xe/m) and for t the time it takes a particle traveling at speed v to cover length l (l/v). Here, the algebraic language allows generation of a new relationship between the distance and quantities other than g and t:
d = (1/2) (Xe/m) (l2/v2) .Finally, algebraic manipulation of this statement allows it to be transformed from a statement about distance to a statement about what Thomson is trying to measure, the charge to mass ratio:
e/m = (2d/X) (v2/l2) .This last statement relates e/m to quantities Thomson could measure in the lab.
[20]It would not be surprising if e/m were found to be independent of speed, for neither the mass nor the charge of an ion depends on speed--at least for ordinary speeds. The fact that there were some variations in the mass of the electron near the speed of light, as documented by Walter Kaufmann's careful measurements published in 1901, was interesting and required explanation. That explanation (and the "other considerations" Thomson mentions here) came in 1905 with Albert Einstein's theory of special relativity. Kaufmann is worth mentioning in an account of the discovery of the electron because he used the very method described here by Thomson to measure e/m of cathode rays in 1897.
[21]Each kind of ion has its own characteristic charge to mass ratio, because each ion has a specific electrical charge and its own characteristic mass. For example, hydrogen ions (H+) all carry a particular amount of charge and have a particular mass, resulting in a characteristic e/m ratio; sodium ions (Na+) carry the same charge as hydrogen ions, but have a greater weight, and therefore a smaller characteristic e/m ratio.
Thomson found that cathode rays always had the same e/m ratio, no matter what metals were used for the cathodes and no matter what gas was used in the tubes. Kaufmann concluded that the hypothesis that cathode rays were particles was inconsistent with this result. Thomson had already been convinced by the preceding evidence that the rays were particles; as we will see, he took the constancy of e/m as evidence that the rays are fragments common to all the gases.
[22]Rubidium (Rb), sodium (Na), and potassium (K) are all in the same column in the periodic table, and belong to the family of alkali metals. So it is not surprising that they have similar properties. In fact, one of the characteristics of that column of the table is the relative ease with which those atoms lose a single electron.
[23]Thomson did not discover the thermoelectric and photoelectric phenomena he just mentioned (i.e., the phenomena in which particles are ejected from hot bodies or metals exposed to light). He did, however, show that the particles involved in these phenomena are the same as cathode rays [Thomson 1899].
[24]By the time of this address, the radioactive fragments which had been labeled β [Rutherford 1899] had already been identified as electrons.
[25]From his earliest characterization of cathode rays, Thomson argued that they were building blocks of atoms [Thomson 1897a], and he elaborated that idea considerably by the time of this address. As early as 1897, he suggested a link between the arrangement of electrons in atoms and the periodicity of atomic properties [Thomson 1897b] (albeit not the link generally recognized today). In 1899 he proposed that ions, charged atoms, acquire their charge by the detachment and attachment of electrons [Thomson 1899]. In 1904 he attempted to explain atomic spectra in terms of the oscillations of electrons in atoms [Thomson 1904]. And in 1906 he argued that the number of electrons in an atom was of the same order of magnitude as its atomic weight (not thousands of electrons per atom, as had been thought up to that point) [Thomson 1906a]. Helge Kragh argues convincingly that Thomson believed that atoms were made up of some sort of corpuscle long before 1897. [Kragh 1997] It is therefore not surprising that Thomson was so prepared to identify the newly characterized cathode particles as one of the constituents of atoms and to construct structural models based on them.
[26]Scottish physicist Charles Thomson Rees Wilson (1869-1959; see biographical sketch at Nobel Foundation) was awarded the Nobel Prize in physics in 1927 for his invention and further development of the cloud chamber (which Thomson describes in some detail here). Wilson was a student of Thomson. He developed the tool for measuring the charge on ions produced by X-rays.
In this brief address, Thomson has mentioned two instances of how the development of tools allowed his research to progress: the cloud chamber and vacuum technology. Technology frequently does assist the progress of science in this way, even if the opposite relationship, the role of science in advancing technology, is more widely known.
[27]Keep in mind that Thomson worked in England; he was very familiar with the phenomena of fog and rain!
[28]The process of rapid expansion cools the moist air. If any dust is present, tiny droplets will form on the dust particles, and carry them to the bottom of the container. The expansion (cooling) is repeated until all the dust has settled at the bottom of the container, carried down by droplets.
[29]When radium, a radioactive element which can ionize (electrify) the air, is introduced, a dense "cloud" is observed to form in dust-free air. Thomson asserts that the cloud is due to the presence of charged particles. How does he know? He can remove the charged particles, and when he does, he greatly reduces the extent of cloud formation.
[30]Now the experiment passes from the qualitative to the quantitative. So far, Thomson has explained how the cloud chamber can be used to detect and visualize charged particles: the visible droplet which forms in dust-free air is like a tag on the invisible charged particle. But the technique can provide even more information: by carefully controlling the amount of supersaturation, one can figure out how much water is contained in the "cloud" droplets; by measuring the speed at which the droplets fall, one can compute the size of the droplets; this information allows computation of the number of droplets. The assumption, as yet unstated but addressed below, is that the number of droplets is the same as the number of charged particles.
[31]From the number of particles and the total charge (obtained from other electrical measurements), one can determine the charge per particle. Thomson made this determination in 1899 [Thomson 1899].
[32]According to a European legend foreign to Islamic tradition, the coffin of the prophet Mohammad (Mahomet) was suspended by magnets in the middle of his tomb. Apparently this story was well enough known in England that figures as different as Thomson just after the 19th century and Mary Wollstonecraft just before it (Vindication of the Rights of Woman, 1792) could refer to it in such a casual way.
[33]Once again Thomson raises possible objections to his experiments and answers them. Here the question is how he knew that the droplets were forming on single charged particles rather than clusters of them, and how he knew the charge was that of an electron rather than an ionized gas molecule.
[34]In fact, the charge of the electron is a fundamental unit of electrical charge. It turns out that the positive building block of atoms, the proton, has the same amount of charge but with the opposite sign. The charges of ions are whole-number multiples of this fundamental charge.
[35]Here Thomson concludes the proof of the argument he made above: the very large e/m of the electron is due to an ordinary charge and a very small mass, much smaller than that of the lightest atom.
[36]Thomson's specialty was the conduction of electricity through gases. The electricity was carried by particles of negative charge and also by particles of positive charge. In gases, the negative charges were all alike (electrons), but the positive charges varied in mass and charge depending on (among other things) what gas was present. These positive ions are what is left of an atom or molecule of the gas after one or more electrons are removed.
 Back to the top of the table of contents of Elements and Atoms.
Back to the top of the table of contents of Elements and Atoms. Back to the top of Classic Chemistry.
Back to the top of Classic Chemistry.