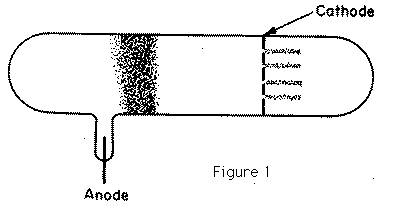
In 1886, Goldstein observed that when the cathode in a vacuum tube was pierced with holes, the electrical discharge did not stop at the cathode; behind the cathode, beams of light could be seen streaming through the holes in the way represented in Figure 1. He ascribed these pencils of light to rays passing through the holes into the gas behind the cathode; and from their association with the channels through the cathode he called these rays Kanalstrahlen. The colour of the light behind the cathode depends on the gas in the tube: with air the light is yellowish, with hydrogen rose colour, with neon the gorgeous neon red, the effects with this gas being exceedingly striking. The rays produce phosphorescence when they strike against the walls of the tube; they also affect a photographic plate. Goldstein could not detect any deflection when a permanent magnet was held near the rays. In 1898, however, W. Wein, by the use of very powerful magnetic fields, deflected these rays and showed that some of them were positively charged; by measuring the electric and magnetic deflections he proved that the masses of the particles in these rays were comparable with the masses of atoms of hydrogen, and thus were more than a thousand times the mass of a particle in the cathode ray. The composition of these positive rays is much more complex than that of the cathode rays, for whereas the particles in the cathode rays are all of the same kind, there are in the positive rays many different kinds of particles. We can, however, by the following method sort these particles out, determine what kind of particles are present, and the velocities with which they are moving. Suppose that a pencil of these rays is moving parallel to the axis of x, striking a plane a right angles to their path at the point O; if before they reach the plane they are acted on by an electric force parallel to the axis of y, the spot where a particle strikes the plane will be deflected parallel to y through a distance y given by the equation
y = (e/mv2) A ,where e, m, v, are respectively the charge, mass, and velocity of the particle, and A a constant depending on the strength of the electric field and the length of path of the particle, but quite independent of e, m, or v.

If the particle is acted upon by a magnetic force parallel to the axis of y, it will be deflected parallel to the axis of z, and the deflection in this direction of the spot where the particle strikes the plane will be given by the equation
z = (e/mv) B ,where B is a quantity depending on the magnetic field and length of path of the particle, but independent of e, m, v. If the particle is acted on simultaneously by the electric and magnetic forces, the spot where it strikes the plane will, if the undeflected position be taken as the origin, have for coordinates
| e | e | ||||
| (1) x = 0, | y = | ---- | A, z = | ---- | B . |
| mv2 | mv |
From equation (1) we see that
| e | B2 | B | |||
| (2) z2 = | -- | y | --- , | z = yv | -- . |
| m | A | A |

A is a large bulb of from 1 to 2 litres capacity in which the discharge passes, C the cathode placed in the neck of the bulb. ...
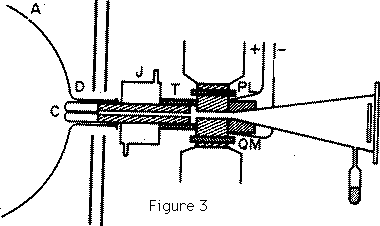
The form of cathode which I have found to give the best pencil of rays is shown in Figure 3. The front of the cathode is an aluminium cap, carefully worked so as to be symmetrical about an axis: this cap fits on to a cylinder made of soft iron with a hole bored along the axis; the object of making the cathode of iron is to screen the rays from magnetic force while they are passing through the hole. A case fitting tightly into this hole contains a long narrow tube which is the channel through which the rays pass into the tube behind the cathode. This tube is the critical part of the apparatus, and failure to obtain a good pencil of rays is generally due to some defect here. As the length of this tube is very long in proportion to its diameter--the length of most of the tubes I have used is about 6 cm. and the diameter from 0.1 to 0.5 mm.--it requires considerable care to get it straight enough to allow an uninterrupted passage to the rays. ... It is useless to attempt to experiment with positive rays unless this tube is exceedingly straight. The rays themselves exert a sand blast kind of action on the tube and disintegrate the metal; after prolonged use the metallic dust may accumulate to such an extent that the tube gets silted up, and obstructs the passage of the rays. The cathode is fixed into the glass vessel by a little wax; the joint is made tight so that the only channel of communication from one side of the cathode to the other is through the tube in the cathode. The wax joint is surrounded by a water jacket J to prevent the wax being heated by the discharge. The arrangements used to produce the electric and magnetic fields to deflect the rays are shown at L and M. An ebonite tube is turned so as to have the shape shown in Figure 3, L and M are two pieces of soft iron with carefully worked plane faces, placed so as to be parallel to each other, these are connected with a battery of storage cells and furnish the electric field. P and Q are the poles of an electromagnet separated from L and M by the thin walls of the ebonite box: when the electromagnet is in action there is a strong magnetic field between L and M; the lines of magnetic force and electric force are by this arrangement parallel to each other and the electric and magnetic fields are as nearly as possible coterminous. ... Plates of soft iron are placed between the electromagnet and the discharge tube to prevent the discharge from being affected by the magnetic field.
The pressure in the tube behind the cathode must be kept very low, this is done by means of a tube containing charcoal cooled by liquid air. The pressure on the other side of the cathode is much higher. ...
The parabolas are determined by the values of e/m, thus an atom with a single charge would produce the same parabola as a diatomic molecule with a double charge. We can, however, by the following method distinguish between parabolas due to particles with a single charge and those due to particles with more than one charge.
The parabolas are not complete parabolas, but arcs starting at a finite distance from the vertical, this distance is by equation (1) inversely proportional to the maximum kinetic energy possessed by the particle. This maximum kinetic energy is that due to the charge on the particle falling from the potential of the anode to that of the cathode in the discharge tube. Consider now the particles which have two charges: these acquire in the discharge tube twice as much kinetic energy as the particles with a single charge. Some of these doubly charged particles will lose one of their charges while passing through the long narrow tube in the cathode, and will emerge as particles with a single charge; they will, however, possess twice as much kinetic energy as those which have had one charge all the time. Thus the stream of singly charged particles emerging from the tube will consist of two sets, one having twice as much kinetic energy as the other; the particles having twice the kinetic energy will strike the plate nearer to the vertical than the others, and will thus prolong beyond the normal length the arc of the parabola corresponding to the singly charged particle. ...
If the atom acquired more than two charges the prolongation of the atomic line would be still longer. If, for example, it could acquire eight charges it would be prolonged until its extremity was only one-eighth of the normal distance from the vertical. ...
Using this method to distinguish between singly and multiply charged systems we find that the particles which produce the parabolas on the photographic plates may be divided into the following classes:
The production of a charged molecule involves nothing more than the detachment of a corpuscle from the molecule, that of a charged atom requires the dissociation of the molecule as well as the electrification of the atom. ...
The rarity of the doubly charged molecule seems to indicate that the shock which produces the double charge is sufficiently intense to dissociate the molecule into its atoms. The uniformity of the intensity of the parabolas corresponding to the multiply charged atoms shows that they acquire this charge at one operation and not by repeated ionisation on their way to the cathode.
The occurrence of the multiple charge does not seem to be connected with the valency or other chemical property of the atom. ... Elements as different in their chemical properties as carbon, nitrogen, oxygen, chlorine, helium, neon, a new gas whose atomic weight is 22, argon, krypton, mercury, all give multiply charged atoms. The fact that these multiple charges so frequently occur on atoms of the inert gases proves, I think, that they are not produced by any process of chemical combination.
All the results point to the conclusion that the occurrence and magnitude of the multiple charge is connected with the mass of the atom rather than with its valency or chemical properties. We find, for example, that the atom of mercury, the heaviest atom I have tested, can have as many as 8 charges, krypton can have as many as 5, argon 3, neon 2, and so on. There is evidence that when these multiple charges occur the process of ionisation is generally such that the atom starts either with one charge or with the maximum number, that in the ionisation of mercury vapour, for example, the mercury atom begins either with 1 charge or with 8, and that the particles which produce the parabola corresponding to 5 charges, for example, started with 8 and lost 3 of them on its way through the tube in the cathode. ...
Again, in a mixture the presence of one gas is apt to swamp the spectrum of another, necessitating, in many cases, considerable purification of the gas before it can be analysed by the spectroscope. This is not the case to anything like the same extent with the positive rays; with these the presence of other gases is a matter of comparatively little importance.
With regard to the sensitiveness of the positive ray method, I have made, as yet, no attempt to design tubes which would give the maximum sensitiveness, but with the tubes actually in use there is no difficulty in detecting the helium contained in a cubic centimetre of air, even though it is mixed with other gases, and I have not the slightest doubt a very much greater degree of sensitiveness could be obtained without much difficulty.
I will illustrate the use of the method by some applications. The first of these is to the detection of rare gases in the atmosphere. Sir James Dewar kindly supplied me with some gases obtained from he residues of liquid air; the first sample had been treated so as to contain the heavier constituents. The positive-ray photograph gave the lines of xenon, krypton, argon, and a faint line due to neon; there were no lines on the photograph unaccounted for, and so we may conclude that there are no heavy unknown gases in the atmosphere occurring in quantities comparable with that of xenon. The second sample from Sir James Dewar contained the lighter gases; the photograph shows that, in addition to helium and neon, there is another gas with an atomic weight about 22. This gas has been found in every specimen of neon which has been examined, including a very carefully purified sample prepared by Mr. E. W. Watson and a specimen very kindly supplied by M. Claud, of Paris. ... The substance giving the line 22 also occurs with a double charge, giving a line for which m/e = 11. There can, therefore, I think, be little doubt that what has been called neon is not a simple gas but a mixture of two gases, one of which has an atomic weight about 20 and the other about 22. The parabola due to the heavier gas is always much fainter than that due to the lighter, so that probably the heavier gas forms only a small percentage of the mixture.
 Back to the list of selected historical papers.
Back to the list of selected historical papers. Back to the top of Classic Chemistry.
Back to the top of Classic Chemistry.