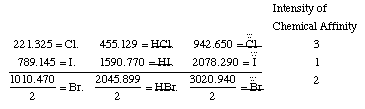
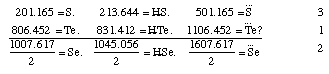
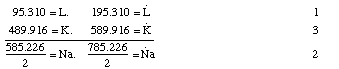
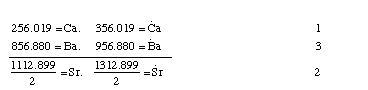
The work of Berzelius on the determination of the atomic weights of bromine and iodine has interested me greatly, since it has established the idea, which I expressed earlier in my lectures, that perhaps the atomic weight of bromine might be the arithmetical mean of the atomic weights of chlorine and iodine. This mean is (35.470+126.470)/2 = 80.470 [sic-- L&K]. This number is not much greater than that found by Berzelius (78.383); however, it comes so close that it may almost be hoped that the difference will vanish entirely after repeated careful and exact determinations of the atomic weights of these three salt-forming elements. This idea was the motive for an attempt which I made twelve years ago to group substances by their analogies. At that time I found that the specific gravity and atomic weight of strontia are very close to the arithmetic mean of the specific gravities and atomic weights of lime and baryta, since
[356.019(=Ca.)+956.880(=Ba.)]/2 = 656.449(=Sr.)and the actual value for strontia is 647.285.[1]
In the alkali group, according to this view, soda stands in the middle, since if we take the value for the atomic weight of lithia, determined by Gmelin, = 195.310, and the value for potash = 589.916, then the arithmetic mean of these numbers,
(195.310+589.916)/2 = 392.613,which comes very close to the atomic value for soda, which Berzelius determined as = 390.897.
For the group including phosphorus and arsenic, the third member is missing. Mitscherlich, the discoverer of isomorphology, will know how to find this if it exists.
If sulfur, selenium, and tellurium belong to one group, which can well be assumed, since the specific gravity of selenium is exactly the arithmetic mean of the specific gravities of sulfur and tellurium, and all three substances combine with hydrogen to form characteristic hydrogen acids, then selenium forms the middle member, since
[32.239(=S) + 129.243(=Te)]/2 = 80.741and the empirically found atomic value for selenium is 79.263.[2]
Fluorine indeed belongs to the salt-forming elements, but certainly not to the group of chlorine, bromine, and iodine; rather to another class of salt-forming substances which perhaps are related to the first as the alkaline earths are to the alkalies. Since it has a very small value, it apparently forms the first member of the assumed group, and in this case there would still be two more members to discover, if triads are actually a law for all groups of chemical substances. If the values shown by the atomic weights of the substances which are here grouped together are compared with the intensity of the chemical affinity which these substances possess, then we find that in the alkalies and alkaline earths the first is directly proportional to the last, but in the salt-forming elements they are inversely proportional. Thus potash, which has the largest value among the alkalies, is the strongest, while lithia, which has the smallest value, is the weakest, and soda, which holds the middle value between potash and lithia, is weaker than potash and stronger than lithia. Baryta, lime, and strontia behave in the same way. However, chlorine, which has the smallest value, is the most powerful, and iodine, which possesses the greatest value, is the weakest in salt formation, and bromine lies between both. If we express the intensity of the chemical affinity of the grouped substances by the numbers 1, 2, and 3, then these considerations can clearly be arranged in the following way:
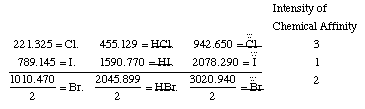
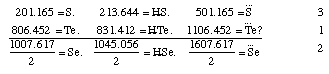
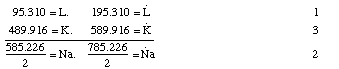
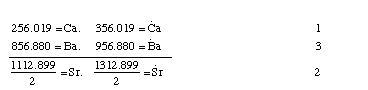
Hydrogen, oxygen, nitrogen, and carbon appear to stand isolated from the substances which form bases, acids, and salts. The fact that the arithmetical mean of the atomic weights of oxygen = 16.026 and carbon 12.256 expresses the atomic weight of nitrogen = 14.138 cannot be considered here, because no analogies occur between these three substances.
The earth metals and the earths themselves belong together, according to their similarities, but I have not yet placed them successfully. It is true that they form boron and silicon, as well as B... and Sl...; aluminum and beryllium, and also Al... and Be...; yttrium and cerium, and also Y. and Ce., which are special groups, but each of them lacks a third member. Magnesium stands entirely alone, and zirconium belongs with titanium and tin.
The group of heavy metal alum-forming substances is fully filled. Its factors are iron oxide Fe..., manganese oxide Mn..., and chromium oxide Cr...; the last apparently forms the middle member, since
(979.426Fe... + 1011.574Mn...)/2 = 995.000Cr... [sic -- L&K]
According to Mitscherlich, Fe., Mn., Ni., Co., Zn., and Cu. are isomorphic with magnesia. This is a highly interesting series of substances, since, first, they all belong to the magnetic metals, and second, they are the best conductors of electricity. But how shall we arrange them if the triad is to be taken as a principle of grouping? In nature, Fe, Mn, and Co occur as oxides which are frequently found together, and the oxides of Ni, Zn, and Cu, as an Englishman says, occur together in an ore from which the Chinese prepare their white copper, which the Germans call Argentan. If this is so, then in the first group manganese forms the third member, since
(439.213 Fe. + 468.991 Co.)/2 = 454.102 Mn.and in the second group it is copper which occupies this position, since
(469.675 Ni. + 503.226 Zn.)/2 =486.450 Cu.However, the atomic weight of Cu. is 495.695, and the specific gravity of copper is not the arithmetical mean of the specific gravities of nickle and zinc, and I therefore believe that these six oxides must be grouped in another way. A rigorous experimental revision of the specific gravities and atomic weights will perhaps remove this doubt.
The most interesting series of analogous metals are those which occur in platinum ores, where platinum, palladium, rhodium, iridium, osmium, and pluranium belong. They fall into two groups according to their specific gravities and atomic weights. Platinum, iridium, and osmium belong in the first group, and in the second, palladium, rhodium, and pluranium. (The latter represents osmium, while rhodium corresponds to iridium and palladium to platinum.) For the members of the first group, the atomic weights, according to the most recent work of Berzelius, are as follows: for platinum, 1233.260; for iridium, 1233.260; for osmium, 1244.210. Now, since the specific gravity of iridium is very near the arithmetical mean of the specific gravities of platinum and osmium (the last, according to Berzelius, =10), then iridium must be considered the middle member
(1233.260 + 1244.210)/2 = 1238.735The atomic weights for the members of the second group, according to the same admirable scientist, are, for palladium, 665.840; for rhodium, 651.400. Thus we get, for pluranium, 636.960, if the atomic weight of the latter stands so near the atomic weights of platinum and iridium, and if rhodium is placed in the middle of this group.[3]
The specific gravity and atomic weight of lead are fairly near the arithmetical mean of the specific gravities and atomic weights of silver and mercury, and I therefore believe that these three metals can be placed together.
Whether tin and cadmium, antimony and bismuth, gold and tungsten, or tungsten and tantalum, etc., belong together, and which may be the missing analogous members, I will not venture to decide.
[2]Tellurium certainly has a still higher degree of oxidation than Te... Perhaps it can be converted to Te... under the same conditions in which Mitscherlich has formed Se... from Se. [original note]
[3]The existence of pluranium still remains in some doubt. P. [P. is Poggendorf. This is editor's note from the original journal.--CJG]
 Back to the list of selected historical papers.
Back to the list of selected historical papers. Back to the top of Classic Chemistry.
Back to the top of Classic Chemistry.