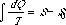 which, while somewhat differently arranged, is the same as that which was formerly used to determine S.
which, while somewhat differently arranged, is the same as that which was formerly used to determine S.Annalen der Physik und Chemie, 125, 353- (1865) [translated and excerpted in William Francis Magie, A Source Book in Physics [New York: McGraw-Hill, 1935]
...
We obtain the equation[1] 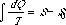 which, while somewhat differently arranged, is the same as that which was formerly used to determine S.
which, while somewhat differently arranged, is the same as that which was formerly used to determine S.
If we wish to designate S by a proper name we can say of it that it is the transformation content of the body, in the same way that we say of the quantity U that it is the heat and work content of the body. However, since I think it is better to take the names of such quantities as these, which are important for science, from the ancient languages, so that they can be introduced without change into all the modern languages, I proposed to name the magnitude S the entropy of the body, from the Greek word η τροπη, a transformation. I have intentionally formed the word entropyso as to be as similar as possible to the word energy, since both these quantities, which are to be known by these names, are so nearly related to each other in their physical significance that a certain similarity in their names seemed to me advantageous.
...
Finally I may allow myself to touch on a matter whose complete treatment would not be in place here, because the statements necessary for that purpose would take up too much room, but of which I believe that even the following short indication will not be without interest, in that it will contribute to the recognition of the importance of the quantities which I have introduced into the formulation of the second law of the mechanical theory of heat. The second law, in the form which I have given it, states the fact that all transformations which occur in nature occur in a certain sense which I have taken as positive, of themselves, that is, without compensation, but that they can only occur in the opposite or negative sense in such a way that they are compensated by positive transformations which occur at the same time. The application of this law to the universe leads to a conclusion to which W. Thomson first called attention and about which I have already spoken in a recently published paper. This conclusion is that if among all the changes of state which occur in the universe the transformations in one sense exceed in magnitude those in the opposite sense, then the general condition of the universe will change more and more in the former sense, and the universe will thus persistently approach a final state.
The question now arises whether this final state can be characterised in a simple and also a definite way. This can be done by treating the transformations, as I have done, as mathematical quantities, whose equivalent values can be calculated and united in a sum by algebraic addition.
In my papers so far published I have carried out such calculations with respect to the heat present in bodies and to the arrangement of the constituents of the bodies. For each body there are found two quantities, the transformation value of its heat content and its disgregration, the sum of which is its entropy. This however does not complete the business. The discussion must also be extended to the radiant heat, or otherwise expressed, to the heat transmitted through the universe in the form of advancing vibrations of the ether, and also to such motions as cannot be comprehended under the name heat.
The treatment of these latter motions, at least as far as they are the motions of ponderable masses, can be briefly settled, since we come by a simple argument to the following conclusion: If a mass, which is so great that in comparison with it an atom may be considered as vanishingly small, moves as a whole, the transformation value of this motion is to be looked on as vanishingly small in the same way in comparison with its kinetic energy; from which it follows that if such a motion is transformed into heat by a passive resistance, then the equivalent value of the uncompensated transformation which then occurs is simply represented by the transformation value of the heat produced. The radiant heat, however, cannot be treated so briefly, since there is need still of a certain special treatment in order to find out how its transformation value is to be determined. Although, in the paper which was recently published and to which I have previously referred, I have already discussed radiant heat in its connection with the mechanical theory of heat, yet I have not as yet treated the question which has here come up, since it was then only my purpose to prove that there was no contradiction between the laws of radiant heat and a fundamental law which I assumed in the mechanical theory of heat. I reserve for future consideration the more particular application of the mechanical theory of heat and especially of the law of equivalents of transformation to radiant heat.
For the present I will confine myself to announcing as a result of my argument that if we think of that quantity which with reference to a single body I have called its entropy, as formed in a consistent way, with consideration of all the circumstances, for the whole universe, and if we use in connection with it the other simpler concept of energy, we can express the fundamental laws of the universe which correspond to the two fundamental laws of the mechanical theory of heat in the following simple form.
1. The energy of the universe is constant.
2. The entropy of the universe tends toward a maximum.
 Back to the list of selected historical papers.
Back to the list of selected historical papers. Back to the top of Classic Chemistry.
Back to the top of Classic Chemistry.