Sir Ernest Rutherford (1871-1937)
Bakerian Lecture: Nuclear Constitution of Atoms
Proc. Roy. Soc. A, 97, 374 (1920). [facsimile from Stephen Wright, Classical Scientific Papers: Physics, (New York: American Elsevier, 1965)]
(Received June 3,-- Lecture delivered June 3, 1920.)
Introduction.-- The conception of the nuclear constitution of atoms arose initially from attempts to account for the scattering of α-particles through large angles in traversing thin sheets of matter.[1] Taking into account the large mass and velocity of the α-particles, these large deflexions were very remarkable, and indicated that very intense electric or magnetic fields exist within the atom. To account for these results, it was found necessary to assume[2] that the atom consists of a charged massive nucleus of dimensions very small compared with the ordinarily accepted magnitude of the diameter of the atom. This positively charged nucleus contains most of the mass of the atom, and is surrounded at a distance by a distribution of negative electrons equal in number to the resultant positive charge on the nucleus. Under those conditions, a very intense electric field exists close to the nucleus, and the large deflexion of the α-particle in an encounter with a single atom happens when the particle passes close to the nucleus. Assuming that the electric forces between the α-particle and the nucleus varied according to an inverse square law in the region close to the nucleus, the writer worked out the relations connecting the number of α-particles scattered through any angle with the charge on the nucleus and the energy of the α-particle. Under the central field of force, the α-particle describes a hyperbolic orbit round the nucleus, and the magnitude of the deflection depends on the closeness of approach to the nucleus. From the data of scattering of α-particles then available, it was deduced that the resultant charge on the nucleus was about (1/2)Ae, where A is the atomic weight and e the fundamental unit of charge. Geiger and Marsden[3] made an elaborate series of experiments to test the correctness of the theory, and confirmed the main conclusions. They found the nucleus charge was about (1/2)Ae, but, from the nature of the experiments, it was difficult to fix the actual value within about 20 per cent. C. G. Darwin[4] worked out completely the deflexion of the α-particle and of the nucleus, taking into account the mass of the latter, and showed that the scattering experiments of Geiger and Marsden could not be reconciled with any law of central force, except the inverse square. The nuclear constitution of the atom was thus very strongly supported by the experiments on scattering of α-rays.
Since the atom is electrically neutral, the number of external electrons surrounding the nucleus must be equal to the number of units of resultant charge on the nucleus. It should be noted that, from the consideration of the scattering of X-rays by light elements, Barkla[5] had shown, in 1911, that the number of electrons was equal to about half the atomic weight. This was deduced from the theory of scattering of Sir J. J. Thomson, in which it was assumed that each of the external electrons in an atom acted as an independent scattering unit.
Two entirely different methods had thus given similar results with regard to the number of external electrons in the atom, but the scattering of α-rays had shown in addition that the positive charge must be concentrated on a massive nucleus of small dimensions. It was suggested by Van den Broek[6] that the scattering of α-particles by the atoms was not inconsistent with the possibility that the charge on the nucleus was equal to the atomic number of the atom, i.e., to the number of the atom when arranged in order of increasing atomic weight. The importance of the atomic number in fixing the properties of an atom was shown by the remarkable work of Moseley[7] on the X-ray spectra of the elements. He showed that the frequency of vibration of corresponding lines in the X-ray spectra of the elements depended on the square of a number which varied by unity in successive elements. This relation received an interpretation by supposing that the nuclear charge varied by unity in passing from atom to atom, and was given numerically by the atomic number. I can only emphasise in passing the great importance of Moseley's work, not only in fixing the number of possible elements, and the position of undetermined elements, but in showing that the properties of an atom were defined by a number which varied by unity in successive atoms. This gives a new method of regarding the periodic classification of the elements, for the atomic number, or its equivalent the nuclear charge, is of more fundamental importance than its atomic weight. In Moseley's work, the frequency of vibration of the atom was not exactly proportional to N, where N is the atomic number, but to (N-a)2, where a was a constant which had different values, depending on whether the K or L series of characteristic radiations were measured. It was supposed that this constant depended on the number and position of the electrons close to the nucleus.
Charge on the Nucleus.-- The question whether the atomic number of an element is the actual measure of its nuclear charge is a matter of such fundamental importance that all methods of attack should be followed up. Several researches are in progress in the Cavendish Laboratory to test the accuracy of this relation. The two most direct methods depend on the scattering of swift α- and β-rays. The former is under investigation, using new methods, by Mr. Chadwick, and the latter by Dr. Crowther. The results so far obtained by Mr. Chadwick strongly support the identity of the atomic number with the nuclear charge within the possible accuracy of the experiment, viz., about 1 per cent.
It thus seems clear that we are on firm ground in supposing that the nuclear charge is numerically given by the atomic number of the element. Incidentally, these results, combined with the work of Moseley, indicate that the law of the inverse square holds with considerable accuracy in the region surrounding the nucleus. It will be of great interest to determine the extent of this region, for it will give us definite information as to the distance of the inner electrons from the nucleus. A comparison of the scattering of slow and swift β-rays should yield important information on this point. The agreement of experiment with theory for the scattering of α-rays between 5° and 150° shows that the law of inverse square holds accurately in the case of a heavy element like gold for distances between about 36x10-12 cm. and 3x10-12 cm. from the centre of the nucleus. We may consequently conclude that few, if any, electrons are present in this region.
An α-particle in a direct collision with a gold atom of nuclear charge 79 will be turned back in its path at a distance of 3x10-12 cm., indicating that the nucleus may be regarded as a point charge even for such a short distance. Until swifter α-particles are available for experiment, we are unable in the case of heavy elements to push further the question of dimensions of heavy atoms. We shall see later, however, that the outlook is more promising in the case of lighter atoms, where the α-particle can approach closer to the nucleus.
It is hardly necessary to emphasise the great importance of the nuclear charge in fixing the physical and chemical properties of an element, for obviously the number and the arrangements of the external electrons on which the great majority of the physical and chemical properties depend, is conditioned by the resultant charge on the nucleus. It is to be anticipated theoretically, and is confirmed by experiment, that the actual mass of the nucleus exercises only a second order effect on the arrangement of the external electrons and their rates of vibration.
It is thus quite possible to imagine the existence of elements of almost identical physical and chemical properties, but which differ from one another in mass, for, provided the resultant nuclear charge is the same, a number of possible stable modes of combination of the different units which make up a complex nucleus may be possible. The dependence of the properties of an atom on its nuclear charge and not on its mass thus offers a rational explanation of the existence of isotopes in which the chemical and physical properties may be almost indistinguishable, but the mass of the isotopes may vary within certain limits. This important question will be considered in more detail later in the paper in the light of evidence as to the nature of the units which make up the nucleus.
The general problem of the structure of the atom thus naturally divides itself into two parts:--
- Constitution of the nucleus itself.
- The arrangement and modes of vibration of the external electrons.
I do not propose to-day to enter into (2), for it is a very large subject in which there is room for much difference of opinion. This side of the problem was first attacked by Bohr and Nicholson, and substantial advances have been made. Recently, Sommerfeld and others have applied Bohr's general method with great success in explaining the fine structure of the spectral lines and the complex modes of vibration of simple atoms involved in the Stark effect. Recently, Langmuir and others have attacked the problem of the arrangement of the external electrons from the chemical standpoint, and have emphasised the importance of assuming a more or less cubical arrangement of the electrons in the atom. No doubt each of these theories has a definite sphere of usefulness, but our knowledge is as yet too scanty to bridge over the apparent differences between them.
I propose to-day to discuss in some detail experiments that have been made with a view of throwing light on the constitution and stability of the nuclei of some of the simpler atoms. From a study of radio-activity we know that the nuclei of the radio-active elements consist in part of helium nuclei of charge 2e. We also have strong reason for believing that the nuclei of atoms contain electrons as well as positively charged bodies, and that the positive charge on the nucleus represents the excess positive charge. It is of interest to note the very different rôle played by the electrons in the outer and inner atom. In the former case, the electrons arrange themselves at a distance from the nucleus, controlled no doubt mainly by the charge on the nucleus and the interaction of their own fields. In the case of the nucleus, the electron forms a very close and powerful combination with the positively charged units and, as far as we know, there is a region just outside the nucleus where no electron is in stable equilibrium. While no doubt each of the external electrons acts as a point charge in considering the forces between it and the nucleus, this cannot be the case for the electron in the nucleus itself. It is to be anticipated that under the intense forces in the latter, the electrons are much deformed and the forces may be of a very different character from those to be expected from an undeformed electron, as in the outer atom. It may be for this reason that the electron can play such a different part in the two cases and yet form stable systems.
It has been generally assumed, on the nucleus theory, that electric forces and charges play a predominant part in determining the structure of the inner and outer atom. The considerable success of this theory in explaining fundamental phenomena is an indication of the general correctness of this point of view. At the same time if the electrons and parts composing the nucleus are in motion, magnetic fields must arise which will have to be taken into account in any complete theory of the atom. In this sense the magnetic fields are to be regarded as a secondary rather than a primary factor, even though such fields may be shown to have an important bearing on the conditions of equilibrium of the atom.
Dimensions of Nuclei.
We have seen that in the case of atoms of large nuclear charge the swiftest α-particle is unable to penetrate to the actual structure of the nucleus so that it is possible to give only a maximum estimate of its dimensions. In the case of light atoms, however, when the nucleus charge is small, there is so close an approach during a direct collision with an α-particle that we are able to estimate its dimensions and form some idea of the forces in operation. This is best shown in the case of a direct collision with an α-particle and an atom of hydrogen. In such a case, the H atom is set in such swift motion that it travels four times as far as the colliding α-particle and can be detected by the scintillation produced on a zinc sulphide screen.[8] The writer[9] has shown that these scintillations are due to hydrogen atoms carrying unit positive charge recoiling with the velocity to be expected from the simple collision theory, viz., 1.6 times the velocity of the α-particle. the relation between the number and velocity of these H atoms is entirely different from that to be expected if the α-particle and H atom are regarded as point charges for the distances under consideration. The result of the collision with swift α-particles is to produce H atoms which have a narrow range of velocity, and which travel nearly in the direction of the impinging particles. It was deduced that the law of inverse squares no longer holds when the nuclei approach to within a distance of 3x10-12 cm. of each other. This is an indication that the nuclei have dimensions of this order of magnitude and that the forces between the nuclei vary very rapidly in magnitude and in direction for a distance of approach comparable with the diameter of the electron as ordinarily calculated. It was pointed out that in such close encounters there were enormous forces between the nuclei, and probably the structure of the nucleus, which may be supposed to consist of four H atoms and two electrons, appeared to survive the collision is an indication that it must be a highly stable structure. Similar results[10] were observed in the collision between α-particles and atoms of nitrogen and oxygen for the recoil atoms appeared to be shot forward mainly in the direction of the α-particles and the region where special forces come into play is of the same order of magnitude as in the case of a collision of an α-particle with hydrogen.
No doubt the space occupied by a nucleus and the distance at which the forces become abnormal increase with the complexity of the nucleus structure. We should expect the H nucleus to be the simplest of all and, if it be the positive electron, it may have exceedingly small dimensions compared with the negative electron. In the collisions between α-particles and H atoms, the α-particle is to be regarded as the more complex structure.
The diameter of the nuclei of the light atoms except hydrogen are probably of the order of magnitude 5x10-13 cm. and in a close collision the nuclei come nearly in contact and may possibly penetrate each other's structure. Under such conditions, only very stable nuclei would be expected to survive the collision and it is thus of great interest to examine whether evidence can be obtained of their disintegration.
In previous papers, loc. cit., I have given an account of the effects produced by close collisions of swift α-particles with light atoms of matter with the view of determining whether the nuclear structure of some of the lighter atoms could be disintegrated by the intense forces brought into play in such close collisions. Evidence was given that the passage of α-particles through dry nitrogen gives rise to swift particles which closely resembled in brilliancy of the scintillations and distance of penetration hydrogen atoms set in motion by close collision with α-particles. It was shown that these swift atoms which appeared only in dry nitrogen and not in oxygen or carbon dioxide could not be ascribed to the presence of water vapour or other hydrogen material, but must arise from the collision of α-particles with nitrogen atoms. The number of such scintillations due to nitrogen was small, viz., about 1 in 12 of the corresponding number in hydrogen, but was two to three times the number of natural scintillations from the source. The number observed in nitrogen was on an average equal to the number of scintillations when hydrogen at about 6 cm. pressure was added to oxygen or carbon dioxide at normal pressure.
While the general evidence indicated that these long range atoms from nitrogen were charged atoms of hydrogen, the preliminary experiments to test the mass of the particles by bending them in a strong magnetic field yielded no definite results.
From the data given in my previous paper (loc. cit.) several theories could be advanced to account for these particles. The calculated range of a singly charged atom set in motion by a close collision with an α-particle of range R cm. in air was shown to be for
| Mass | 1 | Range | 3.91 R |
| " | 2 | " | 4.6 R |
| " | 3 | " | 5.06 R |
| " | 4 | " | 4.0 R |
On account of the small number and weakness of the scintillations under the experimental conditions, the range of the swift atoms from nitrogen could not be determined with sufficient certainty to decide definitely between any of these possibilities. The likelihood that the particles were the original α-particles which had lost one of their two charges, i.e., atoms of charge 1 and mass 4, was suggested by me to several correspondents, but there appeared to be no obvious reason why nitrogen, of all the elements examined, should be the only one in which the passage of a swift α-particle led to the capture of a single electron.
If, however, a sufficient number of scintillations could be obtained under the experimental conditions, there should be no inherent difficulty in deciding between the various possibilities by examining the deflexion of the swift atoms by a magnetic field. The amount of deflexion of charged atoms in a magnetic field perpendicular to the direction of flight is proportional to e/mu. Assuming that the particles were liberated by a direct collision with an α-particle, the relative values of this quantity for different recoiling masses are easily calculated. Taking values MV/E for the α-particle as unity, the corresponding values of mu/e for atoms of charge 1 and mass 1, 2, 3, and 4 are 1.25, 0.75, 0.58, and 0.50 respectively. Consequently the H atoms should be more bent than the α-particles which produced them while the atoms of mass 2 or 3, or 4 would be more difficult to deflect than the parent α-particle.
On my arrival in Cambridge, this problem was attacked in several ways. By the choice of objectives of wide aperture, the scintillations were increased in brilliancy and counting thus made easier. A number of experiments were also made to obtain more powerful sources of radiation with the radium at my command, but finally it was found best, for reasons which need not be discussed here, to obtain the active source of radiation of radium C in the manner described in my previous paper. After a number of observations with solid nitrogen compounds, described later, a simple method was finally devised to estimate the mass of the particle by the use of nitrogen in the gaseous state. The use of the gas itself for this purpose had several advantages over the use of solid nitrogen compounds, for not only was the number of scintillations greater, but the absence of hydrogen or other hydrogen compounds could be ensured.
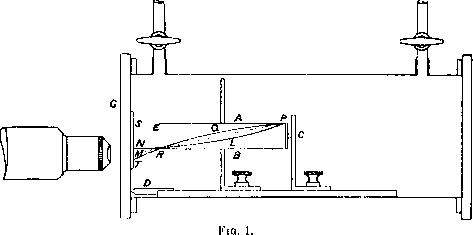
The arrangement finally adopted is shown in fig. 1. The essential point lay in the use of wide slits, between which the α-particles passed. Experiment showed that the ratio of the number of scintillations on the screen arising from the gas to the number of natural scintillations from the source, increased rapidly with increased depth of the slits. For plates 1 mm. apart this ratio was less than unity, but for slits 8 mm. apart the ratio had a value 2 to 3. Such a variation is to be anticipated on theoretical grounds if the majority of the particles are liberated at an angle with the direction of the incident α-particles.
The horizontal slits A, B were 6.0 cm. long, 1.5 cm. wide, and 8 mm. deep, with the source, C of the active deposit of radium placed at one end and the zinc sulphide screen near the other. The carrier of the source and slits were placed in a rectangular brass box, through which a current of dry air or other gas was continuously passed to avoid the danger of radio-active contamination. The box was placed between the poles of a large electro-magnet, so that the uniform field was parallel to the plane of the plates and perpendicular to their length. A distance piece, D, of length 1.2 cm., was added between the source and end of the slits, in order to increase the amount of deflexion of the radiation issuing from the slits. The zinc sulphide screen, S, was placed on a glass plate covering the end of the box. The distance between the source and the screen was 7.4 cm. The recoil atom from oxygen or nitrogen of range 9 cm. could be stopped by inserting an aluminium screen of stopping power about 2 cm. of air placed at the end of the slits.
With such deep slits it was impossible to bend the wide beam of radiation to the sides, but the amount of deflexion of the radiation issuing near the bottom of the slit was measured. For this purpose it was essential to observe the scintillations at a fixed point of the screen near M. The method of fixing the position of the counting microscope was as follows: The source, C, was placed in position, and the air exhausted to a pressure of a few centimetres. Without the field, the bottom edge of the beam was fixed by the straight line PM cutting the screen at M. The microscope was adjusted so that the boundary line of scintillations appeared above the horizontal cross wire in the microscope, marking the centre of the field.
On exciting the magnet to bend the rays upward (called the + field), the path of the limiting α-particles is marked by the curve PLRN cutting the screen at N, so that the boundary of the scintillations appears to be displaced downwards in the field of view. On reversing the field (called the - field), the path of the limiting α-particle PQRT cuts the screen at T, and the band of scintillations appears to be bent upwards. The strength of the magnetic field was adjusted so that, with a negative field, the scintillations were observed all over the screen, while with a positive field, they were mainly confined below the cross wire. The appearance in the field of view of the microscope for the two fields is illustrated in fig. 2, 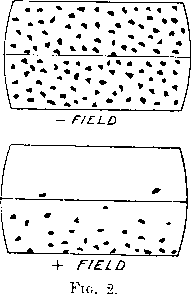 where the dots represent approximately the density of distribution of the scintillations. The horizontal boundaries of the field of view were given by a rectangular opening in a plate fixed in the position of the cross wires. A horizontal wire, which bisected the field of view, was visible under the conditions of counting, and allowed the relative numbers of scintillations in the two halves of the field to be counted if required. Since the number of scintillations in the actual experiments with nitrogen was much too small to mark directly the boundary of the scintillations, in order to estimate the bending of the rays, it was necessary to determine the ratio of the number of scintillations with the + and - field.
where the dots represent approximately the density of distribution of the scintillations. The horizontal boundaries of the field of view were given by a rectangular opening in a plate fixed in the position of the cross wires. A horizontal wire, which bisected the field of view, was visible under the conditions of counting, and allowed the relative numbers of scintillations in the two halves of the field to be counted if required. Since the number of scintillations in the actual experiments with nitrogen was much too small to mark directly the boundary of the scintillations, in order to estimate the bending of the rays, it was necessary to determine the ratio of the number of scintillations with the + and - field.
The position of the microscope and the strength of the magnetic field were in most experiments so adjusted that this ratio was about one-third. Preliminary observations showed that this ratio was sensitive to changes of the field and it thus afforded a suitable method for estimating the relative bending of any radiations under examination.
After the position of the microscope was fixed, air was let in, and a continuous flow of dry air maintained through the apparatus. The absorbing screen was introduced at E to stop the atoms from N and O of range 9 cm. The number of scintillations was then systematically counted for the two directions of the field, and a correction, if required, made for any slight radioactive contamination of the screen. The deflexion due to the unknown radiation was directly compared with that produced by a known radiation of α-rays. For this purpose, after removal of the source and absorbing screen, a similar plate, coated with a weak distribution of the active deposit of thorium, was substituted for the radium source. The α-particles from thorium C of range 8.6 cm. produced bright scintillations in the screen after traversing the 7.4 cm. of air in their path. The ratio of the number of scintillations with + and - fields was determined as before.
An example of such comparison is given below. For a current of 4.0 amp. through the electromagnet, the ratio for particles from nitrogen was found to be 0.33. The corresponding ratio for α-particles from thorium C was 0.44 for a current of 4 amp. and 0.31 for a current of 5 amp. It is thus seen that on the average, the particles from nitrogen are more bent in a given field than the α-particles from thorium C. In order, however, to make a quantitative comparison, it is necessary to take into account the reduction in velocity of the radiations in passing through the air. The value mu/e for the α-ray of range 8.6 cm. from thorium C is known to be 4.28x105. Since the rays pass through 7.4 cm. of air in a uniform field before striking the screen, it can be calculated that the actual deflection corresponds to α-rays in a vacuum for which mu/e = 3.7x105, about. Taking the deflection of the α-particles for a current of 4.8 amp. to be the same as for the nitrogen particles for a field of 4 amp.--ratio of fields 1.17--it is seen that the average deflexion of the nitrogen particles under the experimental conditions corresponds to a radiation in a vacuum for which the value of mu/e = 3.1x105.
Bearing in mind that the particles under examination are produced throughout the volume of the gas between the slits, and that their distribution is unknown, and also that the particles are shot forward on an average at an angle with the incident α-particles, the experimental data are quite insufficient to calculate the average value of mu/e to be expected under the experimental conditions for any assumed mass of projected particles. It seems probable that the majority of the particles which produce scintillations are generated in the first few centimetres of the air next the source. The actual deflection of a given particle by the magnetic field will depend on the distance of its point of origin from the source. These factors will obviously tend to make the average deflection of the particles to appear less than if they were all expelled with constant velocity from the source itself. Assuming that the correction for reduction of velocity of the long range particles in traversing the gas is 10 per cent., the average value of mu/e is about 3.4x105. Since the value of MV/E for the α-particle from radium C is 3.98x105, it is seen that under the experimental conditions the average value of mu/e for the nitrogen particles is less than that of the α-particles which produce them.
From the data given earlier in the paper, this should only be true if the particles are comparable in mass with an atom of hydrogen, for singly charged particles of mass 2, 3, or 4 should suffer less deflexion than the α-particles. For example, if we assume that the particles were helium atoms carrying one charge, we should expect them to be deflected to about one-half of the extent of the α-particle. The experimental results thus afford strong presumptive evidence that the particles liberated from nitrogen are atoms of hydrogen.
A far more decisive test, however, can be made by comparing the deflexion of the nitrogen particles with that of H atoms under similar conditions. For this purpose, a mixture of about one volume of hydrogen to two of carbon dioxide was stored in a gas-holder and circulated in place of air through the testing apparatus. The proportions of the two gases were so adjusted that the stopping power of the mixture for α-rays was equal to that of air. Under these conditions, the H atoms, like the nitrogen particles, are produced throughout the volume of the gas, and probably the relative distribution of H atoms along the path of the α-rays is not very different from that of the nitrogen particles under examination. If the nitrogen particles are H atoms, we should expect the average deflexion to be nearly the same as for the H atoms liberated from the hydrogen mixture. A number of careful experiments showed that the ratio of the umber of scintillations in + and - fields of equal value was so nearly identical in the two cases that the experiments were unable to distinguish between them. Since the two experiments were carried out under as nearly as possible identical conditions, the equality of the ratio shows that the long range particles liberated from nitrogen are atoms of hydrogen. The possibility that the particles may be of mass 2, 3, or 4 is definitely excluded.
In a previous paper I have given evidence that the long range particles observed in dry air and pure nitrogen must arise from the nitrogen atoms themselves. It is thus clear that some of the nitrogen atoms are disintegrated by their collision with swift α-particles and that swift atoms of positively charged hydrogen are expelled. It is to be inferred that the charged atom of hydrogen is one of the components of which the nucleus of nitrogen is built up.
While it has long been known that helium is a product of the spontaneous transformation of some of the radio-active elements, the possibility of disintegrating the structure of stable atoms by artificial methods has been a matter of uncertainty. This is the first time that evidence has been obtained that hydrogen is one of the components of the nitrogen nucleus.
It should be borne in mind that the amount of disintegration effected in nitrogen by the particles is excessively small, for probably on an average only one α-particles in about 300,000 is able to get near enough to he nitrogen nucleus to liberate the atom of hydrogen with sufficient energy to be detected by the scintillation method. Even if the whole α-radiation from 1 gramme of radium were absorbed in nitrogen gas, the volume of hydrogen set free would be only about 1/300000 of the volume of helium due to the collected α-particles, viz., about 5x10-4 cub. mm. per year. It may be possible that the collision of an α-particle is effective in liberating the hydrogen from the nucleus without necessarily giving it sufficient velocity to be detected by scintillations. If this should prove to be the case, the amount of disintegration may be much greater than the value given above.
Experiments with Solid Nitrogen Compounds.
A brief account will now be given of experiments with solid nitrogen compounds. Since the liberation of the particle from nitrogen is a purely atomic phenomenon, it was to be expected that similar particles would be liberated from nitrogen compounds in number proportional to the amount of nitrogen. To test this point, and also the nature of the particles, a number of compounds rich in nitrogen were examined. For this purpose I have employed the following substances, which were prepared as carefully as possible to exclude the presence of hydrogen in any form:--- Boron nitride, kindly prepared for me by W. J. Shutt, in Manchester University.
- Sodium Nitride, titanium nitride and para-cyanogen, kindly prepared for me by Sir William Pope and his assistants.
The apparatus used was similar in form to that given in fig. 1, except that the plates were 4 cm. long. By means of a fine gauze, the powdered material was sifted as uniformly as possible on a thin aluminium plate about 2 sq. cm. in area. The weight of the aluminium plate was about 6 mgrm. per square centimetre, and usually about 4 to 5 mgrm. of the material per square centimetre was used. The stopping power of the aluminium plate for α-particles corresponded to about 3.4 cm. of air, and it was usually arranged that the average stopping power of the material was about the same as for the aluminium. In order to make the material adhere tightly to the plate, a layer of alcohol was first brushed on and the material rapidly sifted into position, and the plate then dried.
Experiment showed that no detectable hydrogen contamination was introduced by the use of alcohol in this way. The zinc sulphide screen was placed outside the box close to an aluminium plate of stopping power equal to 5.2 cm. of air which covered an opening in the end of the brass box. The aluminium carrier was then placed in position to cover the end of the slits near the source, care being taken not to shake off any material. The air was exhausted and the number of scintillations on the screen counted.
- With material facing the source.
- With plate reversed.
In the former case, the α-particles were fired directly into the material under examination; in the latter case the α-particles only fell on the material when their range was reduced to about half, when their power of liberating swift atoms is much reduced. This method of reversal had the great advantage that no correction was necessary for unequal absorption of the H-particles from the source in different experiments.
In this way it was found that all the nitrogen compounds examined gave a larger number of scintillations in position (1). The nature of these particles was examined by a method similar to that employed in the case of nitrogen and a direct comparison was made of the deflexion of the particles with that of H atoms liberated from a film of paraffin put in place of the nitrogen compound. In all experiments, the particles were found to be deflected to the same degree as H atoms from the paraffin and no trace of particles of mass 2, 3 or 4 was detected.
For films of equal average stopping power for α-rays, it can readily be calculated from Bragg's rule that the relative stopping power of the nitrogen in the compounds is 0.67 for B.N., 0.74 for C2N2, 0.40 for titanium nitride, taking the stopping power of sodium nitride as unity. Since the expulsion of long range nitrogen particles must be an atomic phenomenon, it was to be expected that the number of scintillations under the experimental conditions, after correction for the natural effect from the source, should be proportional to the relative values of stopping power given above. The observations with sodium nitride and titanium nitride were very consistent and the number of long range nitrogen particles was in the right proportion and about the same as that to be expected from the experiments with nitrogen gas. On the other hand, boron nitride and para-cyanogen gave between 1.5 and 2 times the number to be expected theoretically. In these experiments every precaution was taken to get rid of hydrogen and water vapour. Before use, the aluminium plates were heated in an exhausted quartz tube in an electric furnace nearly to its melting point to get rid of hydrogen and other gases. The films under examination were kept in a dessicator and heated in the electric furnace just before use and transferred at once to the testing vessel. Several control experiments were made, using preparations not containing nitrogen, viz. pure graphite and silica which had been kindly prepared for me by Sir William Pope. In both of these cases, the number of scintillations observed with the material facing the α-rays was actually less than when the plate was reversed. This showed that some H atoms were liberated by the α-rays from the heated aluminium. The control experiments were thus very satisfactory in showing that H atoms were not present in materials not containing nitrogen. Incidentally, they show that H atoms do not arise in appreciable numbers from carbon, silicon, or oxygen.
The increased effect in boron nitride and para-cyanogen naturally led to the suspicion that these preparations contained some hydrogen although every precaution was taken to avoid such a possibility. In the case of boron nitride there is also the uncertainty whether boron itself emits H atoms. This point has not yet been properly examined. On account of these uncertainties, experiments on solid nitrogen compounds were abandoned for the time, and experiments already described made directly on gaseous nitrogen.
It is of interest to note that a considerable contamination of hydrogen is required to produce the number of H atoms observed in these compounds. In the case of sodium nitride at least 50 c.c. of hydrogen must be present per gram of material. I am inclined to think that the H atoms liberated by the α-rays from sodium nitride is due mainly, if not entirely to the nitrogen, and in the case of para-cyanogen, part of the effect is probably due to the presence of hydrogen or other hydrogen compound. It is hoped to examine this question in more detail later.
Short Range Atoms from Oxygen and Nitrogen.
In addition to the long range H atoms liberated from nitrogen, the passage of α-particles through oxygen as well as through nitrogen gives rise to much more numerous swift atoms, which have a range in air of about 9.0 cm. compared with that of 7.0 cm. for the colliding α-particles. The method of determining the range and number of these atoms has been explained in a previous paper.[10] It is there shown that these projected atoms arise from the passage of the α-particles through the gas. Just beyond the range of the α-particles from radium C, the scintillations are much brighter than those due to H atoms, and more resemble α-particles.
In the absence of definite information as to the nature of these atoms, it was provisionally assumed that they were atoms of oxygen or nitrogen carrying a single charge set in swift motion by close collisions with α-particles, for the observed range of these particles was in approximate accord with that calculated on these assumptions. At the same time it was pointed out that the agreement of the ranges of the atoms set free in N and O was rather surprising, for it was to be anticipated that the range of the swifter N atoms should be about 19 per cent. greater than for the slower O atoms. The possibility that these swift atoms might prove to be fragments of disintegrated atoms was always present, but up till quite recently, I did not see any method of settling the question.[11]
As soon as the use of wide slits had proved successful in deciding the nature of the long range particles from nitrogen, experiments were made with the same apparatus and method to test the nature of the short range particles in O and N.
First consider the relative deflexion to be expected for an O atom which is set in motion by a direct impact with an α-particle. The velocity of the O atom after the collision is 2/5 V, where V is the velocity of the incident α-particle. The value of mu/e for the O atom carrying a single charge is easily seen to be 3.1 times that of the α-particle before impact. Consequently the O atom with a single charge should be much more difficult to deflect than the α-particle, and this is the case even if the former carries two charges.
To test these points, the apparatus was the same as that shown in fig. 1. The source was 7.4 cm. distant from the zinc sulphide screen, the end pieces, 1.2 cm. long, being used as before to increase the deflexion of the rays. During an experiment, dried air or oxygen was circulated slowly through the apparatus to avoid radio-active contamination of the screen. In the case of oxygen, the scintillations observed on the screen were due to the O atoms with a small proportion of H atoms from the source. In the case of air, the scintillations on the screen were due partly to N atoms, some O atoms, and H atoms from the source and nitrogen. The actual number of short range N atoms appeared to be less than the number of O atoms under similar conditions.
The position of the microscope was fixed as before to give a convenient ratio for the number of scintillations on reversing the magnetic field. This ratio varied with the position of the microscope, and in the actual experiments had values between 0.2 and 0.4.
It was at once obvious that the atoms from O instead of being less deflected than the α-particles, as they should be if they were O atoms, were more deflected. This at once excluded the possibility that the atoms from oxygen were actual atoms of oxygen carrying either one or two charges. Since helium is expelled in so many radio-active changes, it might be expected to be one of the components of light atoms, liberated by the intense collision. The deflexion of the atoms from O was, however, much too large to be accounted for in this way. To test this point, at the conclusion of the experiments with oxygen, a plate which had been exposed to thorium emanation was substituted for the radium source, and the bending of the rays of range 8.6 cm. from thorium C was examined in a similar way. If an α-particle were ejected from an O atom near the source, it would be bent like an α-particle of range 9.0 cm.; if produced near the end of the range of α-rays, the amount of bending could not be more than for an α-particle of range 7.0 cm., i.e., about 9 per cent. more than in the first case. Even supposing the particles were liberated uniformly along the path of the α-rays and moved in the same line as the colliding particle, the average bending would not differ by 5 per cent. from that of the α-particle from thorium C. If, as seems probable, some of the atoms are liberated at an angle with the incident particles, the average amount of bending of the beam would be less than the above, and in all probability less than for the α-particles from thorium C. Actually the bending observed was about 20 per cent. greater, showing that the hypothesis that the atoms from O are charged atoms of helium is quite untenable.
If the atoms from O were H atoms, they would be more bent than the α-particles, but would have a maximum range of 28 cm. instead of the 9.0 cm. observed. It thus seemed clear from this evidence that the atom must be of mass intermediate between 1 and 4, while from consideration of the range of the particles and their amount of deflexion it was clear that the atom carried two units of charge.
In order to make a more decisive test, the deflexion of O atoms in a positive and negative field of given value was directly compared with the deflexion of H atoms from a mixture of hydrogen and carbonic acid, in the ratio of about 1 to 2 in volume. In order to absorb completely the O atoms from CO2, aluminium foil was placed over the zinc sulphide screen, so that the total absorption between the source and screen corresponded to slightly more than 9 cm. or air. In both experiments, the atoms under examination are produced in the gas between the slits, and probably the relative distribution along the path of the α-rays is not markedly different in the two cases.
The ratios for reversing the field in the two experiments were found to be nearly equal; but, as an average of a number of experiments, the H atoms were slightly more bent than the atoms from O. From a number of experiments it was concluded that the difference in deflexion did not on the average amount to more than 5 per cent., although from the nature of the observations it was difficult to fix the difference with any certainty.
From these data and the range of the atoms from O in air, we can deduce the mass of the particle liberated from oxygen.
Let m = mass of the atom from O,
u = its maximum velocity near the source,
E = charge
Let M, V, E be the corresponding values for the incident α-particles and m'u'e the values for the H atoms liberated close to the source.
Taking into account that the particle from O of range 9 cm. is steadily reduced in velocity in passing through the 7.4 cm. of oxygen between the source and screen, it can easily be calculated that its average deflexion by the magnetic field is proportional to 1.14 E/mu in place of E/mu in a vacuum.
In a similar way, the deflexion of the H atom is proportional to 1.05 e/m'u', the correction in this case for change of velocity being smaller, and estimated to be about 5 per cent. Now we have seen that the experimental results showed that the atom from O were bent about 5 per cent. less than the H atoms. Consequently
1.14E/mu = (1.05/1.05)(e/m'u') = 1.25E/mv,
or 1.14MV = 1.25mu, (1)
since it has been calculated and verified by experiment that the deflexion of the H atom in a magnetic field is 1.25 times that of the α-particle which sets it in motion (see Paper II, loc. cit.). Also in a previous paper, III, velocity u, carrying a double charge, is given by x/R = (m/M)(u/V)3 ,
where R is the range of the α-particle of mass M and velocity V. Since x = 9.0 cm. for the atoms from O set in motion by collision with α-particles from radium C of range 7 cm., x/R = 1.29 ,
and taking M = 4 mu3 = 5.16v3. (2)
A formula of this type has been shown to account for the range of the H atom, and there is every reason to believe it is fairly accurate over such a short difference of range.
From (1) and (2)
u = 1.19V,
m = 3.1.
Considering the difficulty of obtaining accurate data, the value m = 3.1 indicates that the atom has a mass about 3 and this value will be taken as the probable value in later discussions.
When air was substituted for oxygen it was not possible to distinguish any difference between the bending of the short range atoms in the two cases. Since the short range atoms from air arise mainly from the nitrogen, we may consequently conclude that the short range atoms liberated by the passage of particles through oxygen or nitrogen consist of atoms of mass 3, carrying a double charge, and initially projected with a velocity 1.19V, where V is the velocity of the colliding α-particle.
There seems to be no escape from the conclusion that these atoms of mass 3 are liberated from the atoms of oxygen or nitrogen as a result of an intense collision with an α-particle. It is thus reasonable to suppose that atoms of mass 3 are constituents of the structure of the nuclei of the atoms of both oxygen and nitrogen. We have shown earlier in the paper that hydrogen is also one of the constituents of the nitrogen nucleus. It is thus clear that the nitrogen nucleus can be disintegrated in two ways, one by the expulsion of an H atom and the other by the expulsion of an atom of mass 3 carrying two charges. Since now these atoms of mass 3 are five to ten times as numerous as the H atoms, it appears that these two forms of disintegration are independent and not simultaneous. From the rareness of the collisions it is highly improbable that a single atom undergoes both types of disintegration.
Since the particles ejected from O and N are not produced at the source, but along the path of the α-particles, it is difficult to determine the deflection of O atoms released from a mica plate placed over the source. In consequence of hydrogen in combination in the mica, the H atoms falling on the screen were so numerous compared with the O particles, and their deflexion under the experimental conditions so nearly alike, that it was difficult to distinguish between them.
Energy Considerations.
In close collisions between an α-particle and an atom, the laws of conservation of energy and of momentum appear to hold,[12] but, in cases where the atoms are disintegrated, we should not necessarily expect these laws to be valid, unless we are able to take into account the change of energy and momentum of the atom in consequence of its disintegration.
In the case of the ejection of a hydrogen atom from the nitrogen nucleus, the data available are insufficient, for we do not know with certainty either the velocity of the H atom or the velocity of the α-particle after the collision.
If we are correct in supposing that atoms of mass 3 are liberated from O and N atoms, it can be easily calculated that there is a slight gain of energy as a result of the disintegration. If the mass is 3 exactly, the velocity of escape of the atom is 1.20 V, where V is the velocity of the impinging α-particle.
Thus,
energy of liberated atom/energy of α-particle = 3x1.44/4 = 1.08,
or there is a gain of 8 per cent. in energy of motion, even though we disregard entirely the subsequent motion of the disintegrated nucleus or of the colliding α-particle. This extra energy must be derived from the nitrogen or oxygen nucleus in the same way that the α-particle gains energy of motion in escaping from the radio-active atom.
For the purpose of calculation, consider a direct collision between an α-particle and an atom of mass 3. The velocity of the latter is 8/7 V, where V is the velocity of the α-particle, and its energy is 0.96 of the initial energy of the α-particle. No doubt, in the actual case of a collision with the O or N atom, in which the atom of mass 3 is liberated, the α-particle comes under the influence of the main field of the nucleus, as well as of that of the part of mass 3 immediately in its path. Under such conditions, it is not to be expected that the α-particle can give 0.96 of its energy to the escaping atom, but the latter acquires additional energy due to the repulsive field of the nucleus.
In our ignorance of the constitution of the nuclei and the nature of the forces in their immediate neighbourhood, it is not desirable to enter into speculations as to the mechanism of the collision at this stage, but it may be possible to obtain further information by a study of the trails of α-particles through oxygen or nitrogen by the well-known expansion method of C. T. R. Wilson. In a previous paper,[13] I discussed the photograph obtained by Mr. Wilson, in which there is a sudden change of 43° in the direction of the trail, with the appearance of a short spur at the fork. Evidence was given that the relative length of the tracks of the α-particle and of the spur were in rough accord with the view that the spur was due to the recoiling oxygen atom. This is quite probably the case, for the general evidence shows that the atoms of mass 3, after liberation, travel nearly in the direction of the α-particle, and an oblique collision may not result in the disintegration of the atom.
Recently, Dr. Shimizu, of the Cavendish Laboratory, has devised a modification of the Wilson expansion apparatus, in which expansions can be periodically produced several times a second, so that the trails of many particles can be inspected in a reasonable time. Under these conditions, both Shimizu and myself saw on several occasions what appeared to be branching trails of an α-particle in which the lengths of the two tracks were comparable. Eye observations of this kind are too uncertain to regard them with much confidence, so arrangements are being made by Mr. Shimizu to obtain photographs, so that the tracks can be examined in detail at leisure. In this way we may hope to obtain valuable information as to the conditions which determine the disintegration of the atoms, and on the relative energy communicated to the three systems involved, viz., the α-particle, the escaping atom, and the residual nucleus.
So far no definite information is available as to the energy of the α-particle required to produce disintegration, but the general evidence indicates that fast α-particles, of range about 7 cm. in air, are more effective than α-particles of range about 4 cm. This may not be connected directly with the actual energy required to effect the disintegration of the atom itself, but rather to the inability of the slower α-particle under the repulsive field to approach close enough to the nucleus to be effective in disrupting it. Possibly the actual energy required to disintegrate the atom is small compared with the energy of the α-particle.
If this be the case, it may be possible for other agents of less energy than the α-particle to effect the disintegration. For example, a swift electron may reach the nucleus with sufficient energy to cause its disintegration, for it moves in an attractive and not a repulsive field as in the case of the α-particle. Similarly, a penetrating γ-ray may have sufficient energy to cause disintegration. It is thus of great importance to test whether oxygen or nitrogen or other elements can be disintegrated under the action of swift cathode rays generated in a vacuum tube. In the case of oxygen and nitrogen, this could be tested simply by observing whether a spectrum closely resembling helium is given by the gas in the tube, after an intense bombardment of a suitable substance, by electrons. Experiments of this type are being undertaken by Dr. Ishida in the Cavendish Laboratory, every precaution being taken by the heating of the vacuum tube of special glass and electrodes to a high temperature to ensure the removal of any occluded helium which may be initially in the material. Helium has previously been observed by several investigators in vacuum tubes and is known to be released from substances by bombardment with cathode rays. The proof of the actual production of helium in such cases is exceedingly difficult, but the recent improvements in vacuum tube technique may make it easier to give a decisive answer to this important question.
Properties of the new Atom.
We have shown that atoms of mass about 3 carrying two positive charges are liberated by α-particles both from nitrogen and oxygen, and it is natural to suppose that these atoms are independent units in the structure of both gases. Since probably the charged atom during its flight is the nucleus of a new atom without any external electrons, we should anticipate that the new atom when it has gained two negative electrons should have physical and chemical properties very nearly identical with those of helium, but with a mass 3 instead of 4. We should anticipate that the spectrum of helium and this isotope should be nearly the same, but on account of the marked difference in the relative masses of the nuclei, the displacement of the lines should be much greater than in the case of isotopes of heavy elements like lead.
It will be remembered that Bourget, Fabry, and Buisson,[14] from an examination of the width of the lines in the spectrum of nebulae, conclude that the spectrum arises from an element of atomic mass about 2.7 or 3 in round numbers. It is difficult, however, on modern views to suppose that the spectrum of the so-called "nebulium" can be due to an element of nuclear charge 2 unless the spectrum under the conditions existing in nebulae are very different from those observed in the laboratory. The possible origin of the spectrum of nebulium has been discussed at length by Nicholson[15] on quite other lines, and it is not easy at the moment to see how the new atoms from oxygen or nitrogen can be connected with the nebular material.
Since probably most of the helium in use is derived, either directly or indirectly, from the transformation of radio-active materials, and these, as far as we know, always give rise to helium of mass 4, the presence of an isotope of helium of mass 3 is not likely to be detected in such sources. It would, however, be of great interest to examine whether the isotope may be present in cases where the apparent presence of helium is difficult to connect with radio-active material; for example, in beryl, drawn attention to by Strutt.[16] This is based on the assumption that the atom of mass 3 is stable. The fact that it survives the intense disturbance of its structure due to a close collision with an α-particle is an indication that it is a structure difficult to disintegrate by external forces.
Constitution of Nuclei and Isotopes.
In considering the possible constitution of the elements, it is natural to suppose that they are built up ultimately of hydrogen nuclei and electrons. On this view the helium nucleus is composed of four hydrogen nuclei and two negative electrons with a resultant charge of two. The fact that the mass of the helium atom 3.997 in terms of oxygen 16 is less than the mass of 4 hydrogen atoms, viz., 4.032, has been generally supposed to be due to the close interaction of the fields in the nucleus resulting in a smaller electromagnetic mass than the sum of the masses of the individual components. Sommerfeld[17] has concluded from this fact that the helium nucleus must be a very stable structure which would require intense forces to disrupt it. Such a conclusion is in agreement with experiment, for no evidence has been obtained to show that helium can be disintegrated by the swift α-particles which are able to disrupt the nuclei of nitrogen and oxygen. In his recent experiments on the isotopes of ordinary elements Aston[18] has shown that within the limit of experimental accuracy the masses of all the isotopes examined are given by whole numbers when oxygen is taken as 16. The only exception is hydrogen, which has a mass 1.008 in agreement with chemical observations. This does not exclude the probability that hydrogen is the ultimate constituent of which nuclei are composed, but indicates that either the grouping of the hydrogen nuclei and electrons is such that the average electromagnetic mass is nearly 1, or, what is more probable, that the secondary units, of which the atom is mainly built up, e.g., helium or its isotope, have a mass given nearly by a whole number when O is 16.
The experimental observations made so far are unable to settle whether the new atom has a mass exactly 3, but from the analogy with helium we may expect the nucleus of the new atom to consist of three H nuclei and one electron, and to have a mass more nearly 3 than the sum of the individual masses in the free state.
If we are correct in this assumption it seems very likely that one electron can also bind two H nuclei and possibly also one H nucleus. In the one case, this entails the possible existence of an atom of mass nearly 2 carrying one charge, which is to be regarded as an isotope of hydrogen. In the other case, it involves the idea of the possible existence of an atom of mass 1 which has zero nucleus charge. Such an atomic structure seems by no means impossible. On present views, the neutral hydrogen atom is regarded as a nucleus of unit charge with an electron attached at a distance, and the spectrum of hydrogen is ascribed to the movements of this distant electron. Under some conditions, however, it may be possible for an electron to combine much more closely with the H nucleus, forming a kind of neutral doublet. Such an atom would have very novel properties. Its external field would be practically zero, except very close to the nucleus, and in consequence it should be able to move freely through matter. Its presence would probably be difficult to detect by the spectroscope, and it may be impossible to contain it in a sealed vessel. On the other hand, it should enter readily the structure of atoms, and may either unite with the nucleus or be disintegrated by its intense field, resulting possibly in the escape of a charged H atom or an electron or both.
If the existence of such atoms be possible, it is to be expected that they may be produced, but probably only in very small numbers, in the electric discharge through hydrogen, where both electrons and H nuclei are present in considerable numbers. It is the intention of the writer to make experiments to test whether any indication of the production of such atoms can be obtained under these conditions.
The existence of such nuclei may not be confined to mass 1 but may be possible for masses 2, 3, or 4, or more, depending on the possibility of combination between the doublets. The existence of such atoms seems almost necessary to explain the building up of the nuclei of heavy elements; for unless we suppose the production of charged particles of very high velocities it is difficult to see how any positively charged particle can reach the nucleus of a heavy atom against its intense repulsive field.
We have seen that so far the nuclei of three light atoms have been recognized experimentally as probable units of atomic structure, viz.,
where the subscript represents the mass of the element.
In considering the possible ways in which nuclei can be built up, difficulties at once arise, for many combinations of these units with negative electrons are possible to give an element of the required nuclear charge and mass. In out complete ignorance of the laws of force close to the nuclei, no criterion is available as to the stability or relative probability of the theoretical systems. With the exception of a few elements which can exist in the gaseous state, the possible isotopes of the elements have not yet been settled. When further information is available as to the products of the disintegration of other elements than the two so far examined, and more complete data have been obtained as to the number and mass of the isotopes, it may be possible to deduce approximate rules which may serve as a guide to the mode in which the nuclei are built up from the simpler units. For these reasons it seems premature at this stage to attempt to discuss with any detail the possible structure of even the lighter and presumably less complex atoms. It may, however, be of some interest to give an example to illustrate a possible method of the formation of isotopes in the case of the lighter elements. This is based on the view that probably in many cases a helium nucleus of mass 4 may be substituted in the complex structure for the corresponding nucleus of mass 3 without seriously interfering with the stability of the system. In such a case, the nuclear charge remains unchanged but the masses differ by unity.
For example, take the case of lithium of nuclear charge 3 and atomic mass about 7. It is natural to suppose that the nucleus is composed of helium or its isotope of mass 3 with one binding electron. The three possible combinations are shown in fig. 3 (p. 398).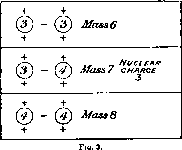
On this view, at least three isotopes of lithium of mass 6, 7, and 8 are theoretically probable, but even if the combinations were equally stable, the question of their relative abundance in the element lithium on the earth will be dependent on many factors of which we known nothing; for example, the mode of actual formation of such nuclei, the relative amount of the combining units present, and the probability of their combinations.
The experimental results given in the paper support, as far as they go, the view that the atoms of hydrogen and of mass 3 are important units in the nuclear structure of nitrogen and oxygen. In the latter case, one could a priori have supposed that oxygen was in some way a combination of four helium nuclei of mass 4. It seems probable that the mass 3 is an important unit of the nuclei of light atoms in general, but it is not unlikely, with increasing complexity of the nuclei and corresponding increase of the electric field, the structures of mass 3 suffer a rearrangement and tend to revert to the presumably more stable nucleus of mass 4. This may be the reason why helium of mass 4 always appears to be expelled from the radio-active atoms, while the isotope of mass 3 arises in the artificial disintegration of lighter atoms like oxygen and nitrogen. It has long been known that for many of the elements the atomic weights can be expressed by the formula 4n or 4n+3, where n is an integer, suggesting that atoms of mass 3 and 4 are important units of the structure of nuclei.[19].
Structure of Carbon, Oxygen, and Nitrogen Nuclei.
In the light of the present experiments, it may be of interest to give some idea, however crude, of the possible formation of the above atoms to account for the experimental facts. It will be remembered that nitrogen alone gives rise to H atoms while carbon and oxygen do not. Both nitrogen and oxygen give rise to atoms of mass 3, while carbon has not yet been investigated from this point of view. A possible structure is shown in fig. 4 when the masses and charges of the combining units are indicated. Negative electrons are represented by the symbol -.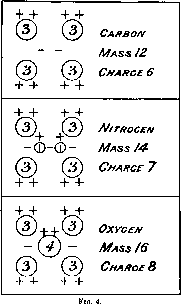
The carbon nucleus is taken to consist of four atoms of mass 3 and charge 2, and two binding electrons. The change to nitrogen is represented by the addition of two H atoms with a binding electron and an oxygen nucleus by the substitution of a helium nucleus in place of the two H atoms.
We can see from this type of structure that the chance of a direct collision with one of the four atoms of mass 3 in nitrogen is much greater than the chance of removing an H atom, for it is to be anticipated that the main nucleus would screen the H atom from a direct collision except in restricted regions facing the H atoms. This serves to illustrate why the number of H atoms of mass 3 liberated from nitrogen should be much greater than the number of H atoms released under corresponding conditions. It should be borne in mind that the structures outlined are purely illustrative and no importance is attached to the particular arrangement employed.
It is natural to inquire as to the nature of the residual atoms after the disintegration of oxygen and nitrogen, supposing that they survive the collision and sink into a new stage of temporary or permanent equilibrium.
The expulsion of an H atom carrying one charge from nitrogen should lower the mass by 1 and the nuclear charge by 1. The residual nucleus should thus have a nuclear charge 6 and mass 13, and should be an isotope of carbon. If a negative electron is released at the same time, the residual atom becomes an isotope of nitrogen.
The expulsion of a mass 3 carrying two charges from nitrogen, probably quite independent of the release of the H atom, lowers the nuclear charge by 2 and the mass by 3. The residual atom should thus be an isotope of boron of nuclear charge 5 and mass 11. If an electron escapes as well, there remains an isotope of carbon of mass 11. The expulsion of a mass 3 from oxygen gives rise to a mass 13 of nuclear charge 6, which should be an isotope of carbon. In case of the loss of an electron as well, there remains an isotope of nitrogen of mass 13. The data at present available are quite insufficient to distinguish between these alternatives.
It is intended to continue experiments, to test whether any evidence can be obtained of the disintegration of other light atoms besides nitrogen and oxygen. The problem is more difficult in the case of elements which cannot be conveniently obtained in the gaseous state, since it is not an easy matter to ensure the absence of hydrogen or to prepare uniform thin films of such substances. For these reasons, and the strain involved in counting scintillations under difficult conditions, further progress is not likely to be rapid.
I am indebted to my assistant, G. A. R. Crowe, for the preparation of the radio-active sources and his help in counting; also to Mr. J. Chadwick and Dr. Ishida for assistance in counting scintillations in some of the later experiments.
[1]Geiger and Marsden, 'Roy. Soc. Proc.,' A, vol. 82, p. 495 (1909).
[2]Rutherford, 'Phil. Mag.,' vol. 21, p. 669 (1911); vol. 27, p. 488 (1914). [Click here for an abstract by Rutherford on this topic.
[3]Geiger and Marsden, 'Phil. Mag.,' vol. 25, p. 604 (1913).
[4]Darwin, 'Phil. Mag.,' vol. 27, p. 499 (1914).
[5]Barkla, 'Phil. Mag.,' vol. 21, p. 648 (1911).
[6]Van den Broek, 'Phys. Zeit.,' vol. 14, p. 32 (1913). [Click here for a similar letter by van den Broek. --CJG]
[7]Moseley, 'Phil. Mag.,' vol. 26, p. 1024 (1913); vol. 27, p. 703 (1914). [Click here for excerpts from these articles. --CJG]
[8]Marsden, 'Phil. Mag.,' vol. 27, p. 824 (1914).
[9]Rutherford, 'Phil. Mag.,' vol. 37, I and II, pp. 538-571 (1919).
[10]Rutherford, 'Phil. Mag.,' vol. 37, III, p. 571 (1919). [However, the next paper in this series describes anomalous results in some scattering of α-particles from nitrogen--evidence of transmutation. --CJG]
[11]Mr. G. S. Fulcher, of the National Research Council, U. S. A., sent me, in November, 1919, a suggestion that these atoms might prove to be α-particles.
[12]Rutherford, 'Phil. Mag.,' vol. 37, p. 562 (1919).
[13]Rutherford, 'Phil. Mag.,' vol. 37, p. 577 (1919).
[14]Bourget, Fabry and Buisson, 'C. R.,' April 6, May 18 (1914).
[15]Nicholson, 'Roy. Ast. Soc.,' vol. 72, No. 1, p. 49 (1911); vol. 74, No. 7, p. 623 (1914).
[16]Strutt, 'Roy. Soc. Proc.,' A, vol. 80, p. 572 (1908).
[17]Sommerfeld, 'Atombau und Spektrallinien,' p. 538. Vieweg and Son, 1919.
[18]Aston, 'Phil. Mag.,' December, 1919: April and May, 1920.
[19]From these and other considerations, Harkins ('Phys. Rev.,' vol. 15, p. 73 (1920)) has proposed a constitutional formula for all the elements. The combining units employed by him are electrons and atoms of mass 1, 3, and 4 of nuclear charges 1, 1 and 2, respectively. The unit of mass 3 is taken by him to have a nucleus charge of 1 and not 2, and is thus to be regarded as an isotope of hydrogen and not an isotope of helium.
 Back to the list of selected historical papers.
Back to the list of selected historical papers.
 Back to the top of Classic Chemistry.
Back to the top of Classic Chemistry.
 Back to the list of selected historical papers.
Back to the list of selected historical papers.